trapez Monia: Proszę o pomoc! Pole trapezu jest równe P , stosunek podstaw trapezu jest 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z nich.

Basia: Pomagam

Eta: OK:

Bogdan: OK.

Eta: Mi wyszło: ^P₉ , ^2P₉, ^2P₉, ^4P₉ czekam na wynik Basi

Eta: O Bogdan Myślałyśmy ,że śpisz już po ciężkiej pracy Czy taka jest odp; do tego zadania?

Bogdan: Ja też mam taki wynik. A przy okazji tego zadania, jeszcze raz przypomnę zadanko na pole trapezu w zależności od pól trójkątów, jakie utworzone są przez przekątne i boki rombu, pamiętacie? P_trapezu = (√P₁ + √P₂)² = P₁ + P₂ + 2√P₁P₂. Ten wzór można wykorzystać przy rozwiązywaniu tego zadanka.

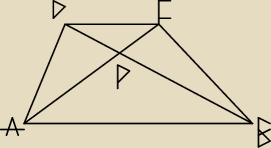
Basia: Trójkaty APB i CPD są podobne

	AB
Skala podobieństwa s=		=2
	CD

P_ABC=s²*P_CPD=4*P_CPD CP=x ⇒ AP=2*CP=2x DP=y ⇒ BP=2*DP=2y

	x*y*sinα
PCPD=
	2

	2x*y*sin(180−α)		x*y*sinα
PAPD=		=2*		=2*PCPD
	2		2

	x*2y*sin(180−α)		x*y*sinα
PBPC=		=2*		=2*PCPD
	2		2

P= P_CPD+P_APB+P_APD+P_BPD= P_CPD+4*P_CPD+2*P_CPD+2*P_CPD=9*P_CPD

	P
PCPD=
	9

	4P
PAPB=
	9

	2P
PAPD=P{BPD}=
	9

Bogdan: Ja rozwiązałem je tak. P − pole trapezu, P₁ − pole dolnego trójkąta, P₂ − pole górnego trójkąta, P₃ − pole lewego oraz pole prawego trójkąta. Skala podobieństwa dolnego do gornago trójkąta k = 2 Wobec tego P₁ = 4P₂, P₃ = √P−1P₂ = √4P₂² = 2P₂ P = P₁ + P₂ + 2P₃ => P = 4P₂ + P₂ + 2*2P₂ = 9P₂ P₂ = ¹₉P P₁ = ⁴₉P P₃ = ²₉P

Bogdan: albo P = (√P₁ + √P₂)² => P = (√4P₂ + √P₂)² => P = (3√P₂)² P = 9P₂ => P₂ = ¹₉P

Basia: Wiedziałam, że wykorzystasz wzór, ale on nie jest, zdaje się, powszechnie znany. Monia musiałaby go najpierw udowodnić. Czy się mylę ?

Bogdan: Masz rację Basiu, ale ja rozwiązywałem teraz dla własnej przyjemności. Monia musiałaby jednak ten wzór wyprowadzić, a przy okazji rozwiązałaby swoje zadanie.

Bogdan: To teraz ja wrzucę zadanko o trapezie. Udowodnić, że w każdym trapezie suma kwadratów długości przekątnych równa się sumie kwadratów długości boków nierównoległych powiększonej o podwójny iloczyn długości podstaw.

Eta: Ja podobnie jak Ty Bogdanie. oczywiście P₁= 4P₂ z podobieństwa natomiast P₃ =P₄= 2P₂ też z podobieństwa, bo ΔAFB i Δ AFD gdzie F − p−t przecięcia przekątnych ,bo mają wspólną wysokość poprowadzoną z wierzchołka A podstawami ich są odcinki BF i FD skoro BF : FD = 2 więc P₃ =P₄= 2P₂ zatem: P= P₁ + P₂ + 2P₃ = 4P₂ +P₂ + 4P₂= 9P₂ dalej juz wiadomo.

Basia: Nie chce mi się rysować. ABCD trapez CC₁ i DD₁ wysokości z tw.cosinusów AC² = AB²+BC²−2AB*BC*cosβ BD² = AB²+AD²−2AB*AD*cosα AC²+BD² = AD²+BC²+2AB²−2AB*AD*cosα−2AB*BC*cosβ= AD²+BC²+2AB(AB − AD*cosα−BC*cosβ)

	AD1
cosα=
	AD

	BC1
cosβ=
	BC

AC²+BD²=AD²+BC²+2AB(AB − AD₁−BC₁)=AD²+BC²+2AB*CD c.b.d.o.

Eta: Ja już mam rozwiązanie pisać? ten dowód?

Eta: To ja daję inny sposób

Basia: A teraz pora spać! Dobranoc wszystkim!

Basia: Dawaj ! Jeszcze poczytamy !

Eta: d₁² = h² +(a−x)² x −−− odcinek odcięty na podstawie "a" d₂² = h² +(a−y)² y −−− podobnie k² = h² +x² l² = h² +y² x+y= a − b d₁² +d₂² = 2h² +2a² +x² +y² − 2ax − 2ay d₁² +d₂² = k² − x² +l² − y² +2a² +x² +y² −2a(x +y) d₁² +d₂² = k² +l² +2a² −2a( a−b) d₁² +d₂² = k² +l² +2ab c.b.d.o Może być ?

Bogdan: Piąteczka Basiu. Też czekam Eto na Twój sposób.

Eta:

Eta: No co tak długo analizujecie ?

Bogdan: No no Eto, również piąteczka. No to po pracowitym dniu pora na zasłużony odpoczynek. Dobranoc

Eta: Dobranoc

Basia: Też piąteczka !

Basia: Dobranoc!

Eta: Miłych snów!

Bogdan: Dzisiaj, a właściwie wczoraj to raczej taki przegadany był dzień, widać było, że dokuczał brak zadań. Za tydzień będzie lepiej.

Bogdan:

Eta: To teraz Wam powiem ,że "Monia" to jaaaaaaaa

Bogdan: Ale nas podeszłaś

Eta: Basia nie miała co robić , więc dlatgo dałam Wam zajęcie Dodranoc!

Bogdan: Basia złakniona zadań pierwsza rzuciła się na pomoc, ale ja też długo nie wytrzymałem, to dla Was

Eta: Dziękujemy , od Nas dla Ciebie.

Eta:

Monia: Chcę powiedzieć,że ku Waszemu zdumieniu znam ten wzór

xpt: Z tego co wiem, to na maturze nie trzeba udowadniać żadnego wzoru, z którego się korzysta, byleby był on prawdziwy.

Basia: Wstrętna oszustka

Eta:

Basia: Przeciwnie, każdy trzeba umieć udowodnić ! Oczywiście nie mówię o wymaganiach szkolnych.

Basia: I byle był w tym zestawie, który CKE opublikowała !

Basia: W przeciwnym wypadku będzie jak z Timem. Czytałeś ?

tim: Ale, że jak..?

tim: A... z tymi wykładnikami pewnie..

Eta:

Basia: Tak Tim, z tymi wykładnikami ! Nie było w programie ⇒ używanie surowo wzbronione i karane Nie do wiary, a prawda

tim: Prawda w oczy kole

tim: Słyszałaś, że od tego roku znowu nowa podstawa... Co raz mniej rzeczy musisz umieć po każdym z etapów. Jak ja będę pisał maturę, to będzie ile to jest 2 + 2 * 2 xD

xpt: Jak!? Gdzie!? Co !? Ja bym się do OKE poszedł kłócić ! (w sumie to do OKE mam 3 minuty drogi, jak mi sygnalizacja świetlna będzie na złość czerwone światło wszędzie dawała, więc mógłbym iść z każdą bzdurą :P ). Umieć udowadniać, a udowadniać to dwie różne sprawy, zwłaszcza, że na egzaminach czas się liczy i trzeba go oszczędzać ;)

Basia: Też bym się kłóciła ! Bo to skandal ! xpt. jak będziesz miał całkę do policzenia, w której trzeba pięć razy zastosować regułę de l'Hospitala to nie pisz od razu =1 (na przykład), chociaż wiesz, że 1 bo wczoraj ją liczyłeś. Obleją Cię !