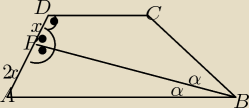
Trapez Ola: W trapezie ABCD (AB||CD) dwusieczna kąta ABC jest prostopadła do ramienia AD trapezu i ma z tym ramieniem punkt wspólny P. Punkt P dzieli ramię AD w stosunku 2:1, licząc od wierzchołka A. Oblicz stosunek pola trójkąta ABP do pola czworokąta PCBD. No to zrobiłam rysunek: i wykombinowałam coś takiego: PΔ=1/2*2x*PB=PBx Potem pole trapezu: P=1/2*x(DC+PB)=1/2xDC+1/2xPB No to kombinuje dalej. Poprowadziłam wysokośc trapezu PCDB z wierzchołka C. Czy tak powstały trójkąt będzie podobny do APB i czy mi się do czegokolwiek przyda? Wiem, że strasznie kombinuję, ale mam już dość geometrii i chcę w końcu zrobić wszystkie zadania Tak więc proszę o wszelkie podpowiedzi

Artur z miasta Neptuna: przeczytaj definicję trapezu −−− dwa boki równoległe ... gdzie masz dwa równoległe boki w czworokącie DPBC

Ola: Ha, faktycznie. Za bardzo się sugerowałam treścią zadania... To w takim razie tym bardziej nie wiem, jak obliczyć pole PBCD.

asdf: czemu przy kącie PDC masz kąt prosty?

Ola: Mój początkowy błąd, tam nie powinno być prostego Ktoś mi podpowie rozwiązanie?

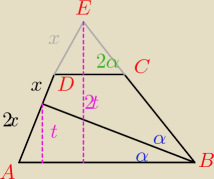Artur z miasta Neptuna: PB = ctgα*AP = 2xctgα P_ΔABP = 2x²ctgα P_□BPDC = P_ΔBPE − P_ΔDCE = 2x²ctgα − P_ΔDCE

	PΔABE
Trójkąt ABE ∼ Trójkąt DCE (podobne trójkąty z proporcją 1:4) ⇒ PΔDCE =
	16

Artur z miasta Neptuna: wracasz do pierwszego Δ:

	|AB|*t		x2ctgα
PΔABP = 2x2ctgα =		⇔ 4x2ctgα = |AB|*t = PΔABE ⇔ PΔABE =
	2		4

i już masz wszystko co chcesz

Ola: t to jest wyskość trójkąta? I skąd mam wiedzieć, że ten drugi odcinek jest róny 2t?

Artur z miasta Neptuna: uproszczając: t = sin β * 2x ... gdzie β = ∡BAP prawda to w takim razie ile wynosi sinβ * 4x 2t A to wynika z 'podobieństwa trójkąta (podstawa "AB" zaczynająca się w A, ograniczona spuszczoną wysokościami −−− czyli trójkąty prostokątne o przeciwprostokątnych 2x i 4x)

Ola: Dla pewności: t to jest wysokość?

Artur z miasta Neptuna: tak ... to jest wysokość trójkąta ABP, spuszczona na |AB|

Ola: Dzięki