Pomocy! Gabrycha: Odcinek AC o końcach A(−4,1) oraz C(2,5) jest przekątną kwadratu ABCD. Wyznacz współrzędne wierzchołków B i D tego kwadratu.

Artur z miasta Neptuna: 1) wyznaczasz wektor AC 2) wyznaczasz równianie prostej zawierającej wektor AC 3) wyznaczasz prostą prostopadłą do wyznaczonej w punkcie (2) 4) wyznaczasz środek wektora AC 5) posta wyznaczona (3) ma przechodzić przez punkt wyznaczony w (4) 6) obliczasz odległość punktu A (lub C) od punktu przecięcia się prostych 7) odznaczasz punkty B i D leżące na prostej wyznaczonej w punkcie (3), odległe od punktu przecięcia o tyle co wyliczyłeś w punkcie (6)

Gabrycha: Jak zrobić punkt 2 ?

Basiek: Dobre pytanie nie jest złe.

Artur z miasta Neptuna: 2) −−− punkt A(−4,1) i C(2,5) mają leżeć na jednej prostej ogólnym równaniu y=ax+b, więc: 1 = a*(−4) + b 5 = a*2 +b rozwiązujesz te układ równań i masz równanie prostej przechodzącej przez punkty A i C ... czyli zawierającej wektor AC

Basiek: Aaaa, czyli posługiwanie się wektorem/ prostą na zmianę. A myślałam, że jest kolejna "fajna" właściwość wektorów Dzięki Artur

Artur z miasta Neptuna: wektor tak naprawdę jest potrzebny tylko do wyznaczenia połowy odcinka AC i ewentualnie odległości krańców wektora do połowy ... i może jeszcze (chociaż niekoniecznie) wyznaczenie współrzędnych środka wektora AC

Artur z miasta Neptuna: z drugiej strony mając wektor [6;4]

	4
wiemy jakie nachylenie będzie mieć prosta zawierająca ten wektor: y =		x + b
	6

ale, aby wyznaczyć 'b' ... musimy podstawić punkt A lub C więc z wektora możesz 'wyłuskać' równanie prostej

Basiek: Tzn. ja "ogarniam" raczej analityczną; zaciekawiło mnie tylko sformułowanie "wyznaczyć równanie prostej zawierającej wektor"

	B
I hm... z tym tgα=		to w sumie TAK BARDZO logiczne, a nigdy bym na to "od tak" nie
	A

wpadła.

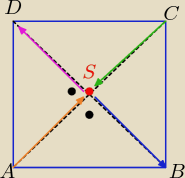
Eta: Można bardzo łatwo rozwiązać to zadanie z wykorzystaniem wektorów A(−4,1) C(2,5) S( −2,3) −−−− to jasne teraz wektory AS=[ 3,2] SD=[−2,3] bo są prostopadłe ( z warunku prostopadłości 3*(−2)+2*3=0 wektory SD=[−2,3] i SB= [2,−3] ,bo są przeciwne i teraz SD=[x_D+1, y_D−3]= [−2,3] ⇒ x_D+1= −2 i y_D−3=3 to D(−3,6) SB= [x_B+1, y_B−3]= [2,−3] ⇒ x_B+1= 2 i y_B−3= −3 to B(1,0) Oczywiście że nad wektorami mają być strzałki

Eta: Echh chochlik oczywiście ,że S(−1,3)

Aga1: Trochę inaczej niż proponuje Artur , niekoniecznie szybciej. 1. Wyznacz współczynnik kierunkowy prostej AC potrzebny do napisania prostej prostopadłej do niej przechodzącej przez punkty BD.

	yC−yA		2
a=		=
	xC−xA		3

2.Wyznacz S−środek odcinka AC

	xA+xC		yA+yC
S=(		,		)=(−1,3)
	2		2

3, Napisz równanie prostej prostopadłej do AC przechodzącej przez punkt S

	−3
y=		x+b
	2

	−3
3=		*(−1)+b
	2

	−3		3
y=		x+
	2		2

4. Punkty Bi D są to punkty wspólne okręgu o środku w punkcie S i promieniu r=IACI i prostej wyznaczonej w punkcie 3. r=IACI=√(2−(−1))²+(5−3)²=√13 równanie okręgu (x+1)²+(y−3)²=13

	−3		3
y=		x+
	2		2

Rozwiązując metodą podstawiania mamy

	−3		3
(x+1)2+(		x−		)2=13
	2		2

	−3
(x+1)2+(		)2(x+1)2=13
	2

13		13
	(x+1)2=13 //:
4		4

(x+1)²=4 Ix+1I=2 x₁=1, x₂=−3 y₁=0, y₂=6 B=(1,0), D=(−3,6)