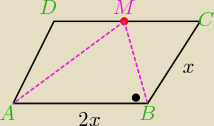
równoległobok asdf: W równoległoboku ABCD , w którym |AB | = 2|AD | punkt M jest środkiem boku CD . Wykaż, że trójkąt ABM jest prostokątny.

asdf: można podpowiedzi jakieś?

rumpek: pomagam

rumpek: zauważ, że trójkąty MCB oraz DMA są równoramienne, oba mają boki x

asdf: to właśnie też zauważyłem

Artur z miasta Neptuna: z tw. cosinusów: |AM|² = x² + x² − 2x*x*cos(∡ADM) = 2x²(1−cos(∡ADM)) |BM|² = x² + x² − 2x*x*cos(∡BCM) = 2x²(1−cos(∡BCM)) zauważasz, że: ∡ADM + ∡BCM = 180^o ... czyli ∡BCM = 180^o − ∡ADM |BM|² = 2x²(1−cos(180 − ∡ADM)) = 2x²(1 + cos(∡ADM)) |AM|² + |BM|² = 2x²(1−cos(∡ADM)) + 2x²(1+cos(∡ADM)) = 4x² z tw. cosinusów: |AB|² = 4x² = |AM|²+|BM|² − 2|AM||BM|cos(∡AMB) ⇔ 4x² = 4x² − 2|AM||BM|cos(∡AMB) ⇔ 2|AM||BM|cos(∡AMB) = 0 ⇔ cos(∡AMB) = 0 ⇔ ∡AMB = 90^o c.n.w.

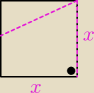
asdf: takie coś mi wyszło, tylko nie wiem co dalej

asdf: ten rysunek wyżej jest zły, x który jest bliżej dwóch przerywanych nie powinno go być... tw cosinusów − tego jeszcze nie robiłem

rumpek: https://matematykaszkolna.pl/forum/131532.html już robiłem

asdf: da się inaczej prócz twierdzeniem cosinusów? w programie nauczania tego nie ma w liceum/technikum dla podstawy

asdf: Dzięki wam

	α
rumpek − tylko dlaczego		?
	2

asdf:

	α		180o − α
reszte rozumiem Tylko dlaczego		a co za tym idzie		.
	2		2

asdf: Teraz rozpatrzmy trójkąt MDA, kąt |∡MDA| = 180o − α (ponieważ w równoległoboku suma kątów ma

	α
miarę 180o). Czyli w trójkącie MDA kąt |∡ADM| = |∡MDA| =
	2

tam nie powinno być w trójkącie?

Aga1: Przez pomyłkę rozwiązałam w innym miejscu z rysunkiem i objaśnieniami. Jeśli jesteś jeszcze zainteresowany to zerknij,tam gdzie rozwiązywał rumpek

rumpek: W równoległoboku kąty przecież przy podstawie są przyległe ... https://matematykaszkolna.pl/strona/3011.html

asdf: no i teraz wszystko jasne dzieki wielkie

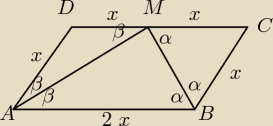
Mila: Kąty naprzemianległe są równe(kąt MAB=katAMD, .......) 2α+2β=180 α+β=90