,..
tatar: Dwie wysokości trójkąta ABC gdzie A(−2,−3) zawarte sa w prostych o równaniu x−2=0 i 2x+3y−1=0
Oblicz wspołrzedne pozostałych wierzchołkow tego trojkata.
AniaS:
X−2=0
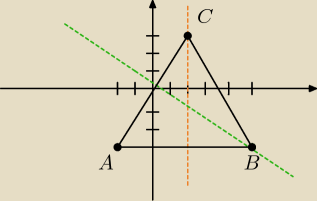
X=2 (pomarańczowa)
2x+3y−1=0
3y=−2x+1 /3
y=−2/3x+1/3 (−1,1), (−4,3) − punkty przez, które przechodzi (zielona)
skoro x=2 ma zawierac wyskoośc trójkąta to wierzchołek B musi znajdowac się na prostej
2x+3y−1=0 i miec tą samą współrzędną y co wierzchołek A:
y=−3
2x+3*(−3)−1=0
2x=10 /2
x=5
B=(−3,5)
obliczam prostą prostopadłą do 2x+3y−1=0 i przechodzącą przec punkt A
y−y
A = a(x−x
A)
a= 3/2
y+3=3/2(x+2)
y=3/2x
obliczam wierzchołek C, który znajduje się na przecięciu prostej y=3/2x i x=2
y=3/2 * 2= 3
C=(2,3)
 X−2=0
X=2 (pomarańczowa)
2x+3y−1=0
3y=−2x+1 /3
y=−2/3x+1/3 (−1,1), (−4,3) − punkty przez, które przechodzi (zielona)
skoro x=2 ma zawierac wyskoośc trójkąta to wierzchołek B musi znajdowac się na prostej
2x+3y−1=0 i miec tą samą współrzędną y co wierzchołek A:
y=−3
2x+3*(−3)−1=0
2x=10 /2
x=5
B=(−3,5)
obliczam prostą prostopadłą do 2x+3y−1=0 i przechodzącą przec punkt A
y−yA = a(x−xA)
a= 3/2
y+3=3/2(x+2)
y=3/2x
obliczam wierzchołek C, który znajduje się na przecięciu prostej y=3/2x i x=2
y=3/2 * 2= 3
C=(2,3)
X−2=0
X=2 (pomarańczowa)
2x+3y−1=0
3y=−2x+1 /3
y=−2/3x+1/3 (−1,1), (−4,3) − punkty przez, które przechodzi (zielona)
skoro x=2 ma zawierac wyskoośc trójkąta to wierzchołek B musi znajdowac się na prostej
2x+3y−1=0 i miec tą samą współrzędną y co wierzchołek A:
y=−3
2x+3*(−3)−1=0
2x=10 /2
x=5
B=(−3,5)
obliczam prostą prostopadłą do 2x+3y−1=0 i przechodzącą przec punkt A
y−yA = a(x−xA)
a= 3/2
y+3=3/2(x+2)
y=3/2x
obliczam wierzchołek C, który znajduje się na przecięciu prostej y=3/2x i x=2
y=3/2 * 2= 3
C=(2,3)