Zadanie Robert: BŁAGAM O POMOC Zad.1. Ostrosłup czworokątny, którego podstawą jest kwadrat o boku 4cm, ma dwie przyległe ściany boczne prostopadłe do płaszczyzny podstawy. Pozostałe dwie ściany boczne sa nachylone do płaszczyzny podstawy pod kątem 45 stopni. Wyznacz cosinus kąta, jaki tworzy najdłuższa krawędź boczna ostrosłupa z płaszczyzną podstawy.

Basia: Pomagam

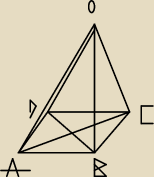Basia: BO prostopadła do pł.podstawy najdłuższa jest DO szukany kąt to α=ODB tr.DBO jest prostokątny BD − przekątna kwadratu BD = a√2 = 4√2

	BD		4√2
cosα=		=
	DO		DO

tr. DCO jest prostokątny kąt DCO kąt prosty CO to jego wysokość czyli kąt BCO=45 tr.CBO też jest prostokątny kąt CBO = 90 kątBCO=45 ⇒kątBOC=45 BO=BC = 4 OC² = BC²+BO² = 16+16 = 32 OC = 4√2 OC² + CD² = OD² 32 + 16 = OD² OD² = 48=16*3 OD = 4√3

	4√2		√2		√6
cosα =		=		=
	4√3		√3		3

o ile nie pomyliłam się w rachunkach na rysunku za bardzo nie widać, że DCO i DAO są prostokatne, ale na modelu z drutu tak