pomoc
oli: wskaz nierownosc ktorej zbiorem rozwiazan jest pzredział (−4, 6)
12 mar 22:32
asdf: x1 = −4
x2 = 6
(x + 4)(x − 6) < 0 ( dla a > 0, w tym przypadku a = 1)
1x2 −2x − 24 < 0
12 mar 22:37
Beti: może być też taka: |x−1| < 5
12 mar 22:39
oli: a to samo tylko <−2, 4>
12 mar 22:41
asdf: Beti, możesz rozpisać swój przykład? Wiem, że tak jest tylko jak do tego dojść

Wiem też, że
odległość od 1 jest mniejsza od 5...tylko jakim to zrobić sposobem

@oli
x
1 = −2
x
2 = 4
(x + 2)(x − 4)
≤ 0
12 mar 22:44
Beti: chodzi Ci asdf o to jak powstała nierówność, czy jak ją rozwiązać?
12 mar 22:49
asdf: Pytanko, jak napiszę to w postaci kanonicznej/iloczynowej to też jest dobrze czy musi być
ogólna

x
2 − 2x + 8 = x
2 − 2x + 4 + 4 = (x − 2)
2 + 4
12 mar 22:50
asdf: jak powstała ta nierówność, rozwiązać to wiem
12 mar 22:50
Beti: a dla przedziału <−2,4> może być np: |x−1| ≤3
12 mar 22:51
asdf: no to powiedz jak to zrobiłaś

12 mar 22:52
Beti: no więc znalazłam środek odcinka o końcach w −4 i 6 − jest nim liczba 1 i określiłam
odległość między liczbami 1 i 6 (5 jedn.) .
Czy takie wyjasnienie wystarczy ?
12 mar 22:55
Aga1:
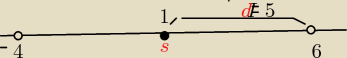
(−4,6)
| | −4+6 | |
s= |
| =1−−−środek przedziału |
| | 2 | |
| | I6−(−4)I | |
d= |
| =5−−−długość połowy przedziału |
| | 2 | |
Ix−sI<d
Ix−1I<5
12 mar 22:57
asdf:
|−4 − 1| = odległość
lub | 6 −1| = odległość
dobrze zrozumiałem?
12 mar 22:59
Beti: tak

12 mar 22:59
asdf: Dzięki Beti i Aga1

(żeby nie było, że aż taki ułom jestem − pisałem swojego posta w trakcie gdy jeszcze nie było
postu Agi

12 mar 23:00
Beti: spoko

12 mar 23:02
 Wiem też, że
odległość od 1 jest mniejsza od 5...tylko jakim to zrobić sposobem
Wiem też, że
odległość od 1 jest mniejsza od 5...tylko jakim to zrobić sposobem  @oli
x1 = −2
x2 = 4
(x + 2)(x − 4) ≤ 0
@oli
x1 = −2
x2 = 4
(x + 2)(x − 4) ≤ 0
 x2 − 2x + 8 = x2 − 2x + 4 + 4 = (x − 2)2 + 4
x2 − 2x + 8 = x2 − 2x + 4 + 4 = (x − 2)2 + 4

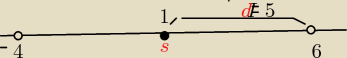 (−4,6)
(−4,6)

 (żeby nie było, że aż taki ułom jestem − pisałem swojego posta w trakcie gdy jeszcze nie było
postu Agi
(żeby nie było, że aż taki ułom jestem − pisałem swojego posta w trakcie gdy jeszcze nie było
postu Agi 
