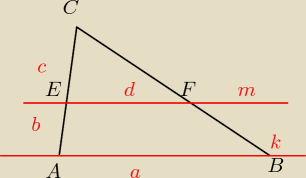
planimetria - pomoc w koncowce zadania jok: W trojkacie ABC poprowadzono prosta m rownolegla do boku AB, ktora przeciela bok AC w punkcie E oraz bok BC w punkcie f, wiedzac ze pole trojkata EFC jest rowne polu trapezu ABFE, wykaz ze U{CE}{EA = √2 + 1 pole trojkata CEF = pole trapezu ABEF pole trojkata ABC = Pole_CEF + Pole_ABEF pole ABC = 2 CEF stosunek CEF do ABC = czyli k², wiec k = √2

a		b+c
	=
d		c

b+c
	= √2
c

√2c = b+c b= c(√2 −1)

c
	= √2 + 1
c(√2−1)

ma to sens? pierwszy raz robie takie cos :Z