| 1 | ||
P= | |(xb−xa)(yc−ya)−(yb−ya)(xc−xa)| | |
| 2 |
| 1 | ||
prostej AB, to będzie Twoja wysokość h. No i ze wzoru P= | *|AB|*h liczymy pole. | |
| 2 |
 Można prościej− ten długi wzór wywodzi się z wyznacznika wektorów, którym robi się o wiele
łatwiej − tu wyjaśnienie tej metody: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .
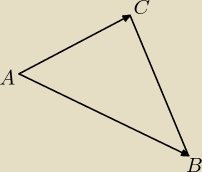
A=(1,−3)
B=(9,1)
C=(5,4)
Liczę współrzędne wektorów:
AB→=[9−1, 1−(−3)]=[8, 4]
AC→=[5−1, 4−(−3)]=[4, 7]
Liczę wyznacznik tych wektorów:
d(AB→, AC→)=
| 8 4 |
| 4 7 |
=8*7−4*4=56−16=40
Można prościej− ten długi wzór wywodzi się z wyznacznika wektorów, którym robi się o wiele
łatwiej − tu wyjaśnienie tej metody: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .
A=(1,−3)
B=(9,1)
C=(5,4)
Liczę współrzędne wektorów:
AB→=[9−1, 1−(−3)]=[8, 4]
AC→=[5−1, 4−(−3)]=[4, 7]
Liczę wyznacznik tych wektorów:
d(AB→, AC→)=
| 8 4 |
| 4 7 |
=8*7−4*4=56−16=40
| 1 | 1 | |||
Pole = | |d(AB→, AC→)|= | *|40|=20 | ||
| 2 | 2 |
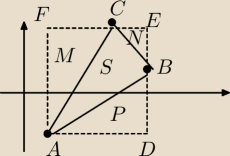 P(ADEF) = AD*DE = 8*7 = 56 j2
M: P1 = 1/2*FC*AF = 1/2*4*7 = 14 j2
N: P2 = 1/2*CE*EB 1/2*4*3 = 6 j2
P: P3 = 1/2*AD*DB = 1/2*8*6 = 16 j2
S = 56 − (14 + 6 + 16) = 56 − 36 = 20 j2
P(ADEF) = AD*DE = 8*7 = 56 j2
M: P1 = 1/2*FC*AF = 1/2*4*7 = 14 j2
N: P2 = 1/2*CE*EB 1/2*4*3 = 6 j2
P: P3 = 1/2*AD*DB = 1/2*8*6 = 16 j2
S = 56 − (14 + 6 + 16) = 56 − 36 = 20 j2