czworoscian foremny Kasia: czworoscian foremny przecieto plaszczyzna przechodzaca przez krawedz podstawy i srodek przeciwleglej krawedzi bocznej. Oblicz cosinus kata zawartego miedzy ta plaszczyzna a podstawa ostroslupa. błagam pomozcie

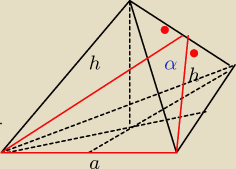
Aga1: Z tw . cosinusów a²=h²+h²−2h*h*cosα

	a√3
gdzie h=
	2

Jakuboo: Płaszczyzna ta stworzy trójkąt o podstawie a i wysokości H. Wierzchołejk tego trójkąta będzie w miejscu a/2, przeciwległej krawędzi. cos alfa to będzie stosunek a/2 do H. Aby obliczyć H przypatrz się temu trójkątowi wewnątrz.. Ma on podstawe a i bok b, gdzie ten bok b jest wysokością trójkąta równobocznego o boku 'a' (ściany bocznej ostrosłupa). Zatem: b =a √3 podzielić przez 2 Z tw. Pitagorasa (dla tego tójkąta wewnątrz), mamy: H²=b²(a/2)² cosα = a/2 podzielić przez H Mnie wyszło ½ . Mam nadzieję, że to chaotyczne tłumaczenie da się zrozumieć.

Aga1: Nie dorysowałam kąta między podstawą a tą płaszczyzną.

Kasia: powinno wyjsc √6 / 3 , a jak robie agi sposobem to mi wychodzi √3 chyba ze zle licze

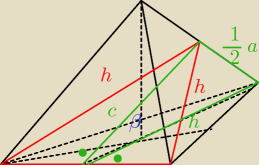
Aga1: Napisałam Ci, że nie zaznaczyłam tego kąta. jest to kąt między wysokością czerwonego trójkąta, a wysokością trójkąta w podstawie. Jak mi się uda to narysuję jeszcze raz . Brakującą wysokość ozn. przez c

	1
c2=h2−(		a}2
	2

	3		1
c2=		a2−		a2
	4		4

	√2
c=a
	2

Z twierdzenia cosinusów

	1
(		a)2=c2+h2−2c*hcosβ
	2

1		2		3		√2		a√3
	a2=		a2+		a2−2*		a*		*cosβ
4		4		4		2		2

a2√6
	cosβ=a2
2

	√6
cosβ=
	3

Aga1:

Aga1: Poszło szybko, a wcześniej czekałam strasznie długo i nie mogłam wysłać.