planimetria
zadanie: W trójkącie ABC o długościach boków |BC|=13, |AC|=14 i |AB|=15, prosta zawierająca dwusieczną
kąta ABC przecina w punkcie D prostą prostopadłą do AC przechodzącą przez punkt C. Oblicz
|CD|.
z tw. o dwusiecznej kata wy;iczam EC=6,5 a co pozniej?
11 mar 22:19
zadanie: 
11 mar 22:34
zadanie:
11 mar 23:27
Mila: EC błędnie wyliczyłeś. Poza tym, dwusieczna jest prawie prostopadła do AC. Czy dobrze zapisałeś
treść?
12 mar 00:02
zadanie: tak
12 mar 00:09
Mila: Masz odpowiedź? Mam dużo rachunków.
12 mar 15:55
zadanie: CD=52
12 mar 17:06
zadanie:
12 mar 17:34
Mila: obliczenia :
AE=7,5
EC=6,5
| | 5 | |
cosγ= |
| z tw. cosinusów |
| | 13 | |
Prowadzę prostopadłą do AC, przechodzącą przez C
Prowadzę odcinek prostopadły do tej prostej BF
Powstaje trapez prostokątny CEFB , KątCBF =γ
obliczam CF i BF
BF=5 (druga podstawa trapezu.
CF=12
x=FD oznaczenie
x=40
CD =52
12 mar 23:11
zadanie: mozna prosic o rysunek
12 mar 23:52
Mila:
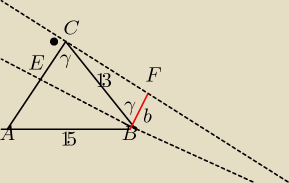
AC=14
Punt D jest poza polem widzenia, dużo niżej.
13 mar 00:10