Ciagi Euklides: Ujemnych wyrazów ciągu określonego wzorem a_n = n² − 2n − 24 jest:

koma: a_n<0 i liczysz

Euklides: wyliczyłem pierwiastki i wyszło, że n₁=−4 − odpada n₂=6 jednak po podstawieniu za n=6 wychodzi, 0 a zero to nie jest liczba ujemna. Ma ktoś pomysł jak to rozwiązać? (oczywiście nie wstawiając pod N po kolei liczb naturalnych )

pigor: ... np. tak : a_n<0 i n∊N ⇒ n²−2n+1−25< 0 ⇔ (n−1)²<25 ⇔ |n−1|< 5 ⇒ −5< n−1<5 i n∊N ⇔ 0< n<6 i n∊N ⇔ n∊{1,2,3,4,5) , czyli 5 wyrazów jest ujemnych . ...

koma: no jest dobrze na paraboli od −4 do 6 przedzial.. ale ze ciag to tylko liczby naturalne dodatnie to nalezy {1,2,3,4,5} czyli 5 wyrazów

koma: ehh...znow sie dzis spoznilem

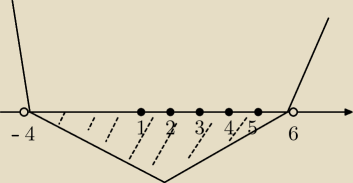
Gustlik: n² − 2n − 24<0 Δ=100, √Δ=10 n₁=−4, n₂=6 Rozwiązaniem nierówności jest przedział (−4, 6), wystarczy teraz wypisać wszystkie liczby naturalne z tego przedziału. Są to liczby 1, 2, 3, 4, 5. Czyli ciąg ma 5 ujemnych wyrazów. Nie przejmuj się, że jeden pierwiastek wyszedł ujemny. Wprawdzie nie spełnia on założeń dla ciagu, ale jest potrzebny do narysowania wykresu i rozwiązania nierówności.