stereometria Tomek: Podstawą ostrosłupa jest trójkąt prostokątny o przeciwprostokątnej długości c i kącie ostrym α. Każda ściana boczna tworzy z podstawą kąt o mierze β. Oblicz pole powierzchni bocznej ostrosłupa.

Tomek: pomógłby ktoś chociaż w rysunku, bo nie wiem czy dobrze zaznaczyłem kąty ?

rumpek: "Jeśli wszystkie ściany bocznej nachylona są do płaszczyzny podstawy ostrosłupa pod tym samym kątem, to spodek wysokości ostrosłupa jest środkiem okręgu wpisanego w podstawę tego ostrosłupa. Wysokości wszystkich ścian bocznych ostrosłupa mają wtedy jednakową długość."

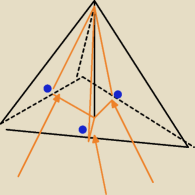
Tomek: tam gdzie poprowadziłem strzałki to kąty β tak?

rumpek: tak

Tomek: o dziękuje Rumpek − już wszytko jasne. Jeżeli mogę wiedzieć to skąd masz to twierdzenie ?

rumpek: to nie twierdzenie to wiedza

rumpek: jakby były krawędzi nachylone do płaszczyzny podstawy, to wtedy spodek byłby na środku przeciwprostokątnej trójkąta

Tomek: to powiedz mi jak miałem do tego dojsc

Tomek: no to z krawędziami wiem

Tomek: dobra juz rozkminilem, dzieki jeszcze raz

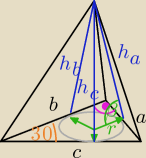
dero2005: dane: c, β

a		1
	= sin 30o =
c		2

	c
a =
	2

b		√3
	= cos 30o =
c		2

	c√3
b =
	2

r − promień okręgu wpisanego

	a+b−c		c   c√3   + − c 2   2		c
r =		=		=		(√3−1)
	2		2		4

h_a = h_b = h_c = h − wysokość ścian bocznych

r
	= cos β
h

	r		c
h =		=		(√3−1)
	cos β		4cos β

	a*h		b*h		c*h		h
Pb =		+		+		=		(a + b + c) =
	2		2		2		2

	c		c		c2√3
=		*(√3−1)[		(√3+3)] =
	8cosβ		2		8 cosβ

Tomek: dero kto powiedział, że tam jest 30^o ? Ale dzięki juz zrobilem to zadanie, analogicznie do Twojego sposobu tylko używałem α−fy.

dero2005: Rzeczywiście, że nie ma napisane, musiałem to sobie wymyslić