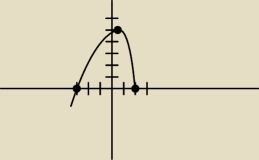
funkcja babeczka: dana jest funkcja f(x)=−x²+x+6, napisz wzór funkcji w postaci kanonicznej i iloczynowej, naszkicuj wykres, podaj zbiór wartości i ekstremum funkcji

babeczka: pomocy

kto: p=−1/2 q=−(− 1/2)²− 1/2 +6 q=5,25 f(x)=−(x+1/2)+5,25 Δ=1−4*6*(−1)=25 x1=−1+5 / 2 x2=−1−5 /2 x1=2 x2=−3 f(x)=−(x−2)(x+3) zw=(−∞;5,25>

babeczka: można jakoś jaśniej?

babeczka: ratunku

babeczka: może ktoś lepiej rozpisać żebym wiedziała o co biega?

Beti: postać kanonizna to: y = a(x−p)²+q zatem potrzebujesz p i q, które obliczysz ze wzorów:

	b		Δ
p = −		q = −
	2a		4a

policz i podstaw

asdf: −x² + x + 6 a = −1 b = 1 c = 6 Liczysz delte, podajesz pierwiastki

	x1 + x2
p =
	2

	−Δ
q =
	4a

wyznaczasz punkt przecięcia się z osią YO = c c = 6 a < 0 (ramiona w dół) postać kanoniczna a(x − p)² + q postać iloczynowa a(x − x₁)(x − x₂) ZWF ( − ∞ (bo a < 0; q) Ekstremum funkcji (w przypadku paraboli jest q (a < 0)) − tego nie jestem do końca pewien (patrz: ekstremum funkcji)