wykes funkcji
Daniel: Punkty równoodlegle od prostej o równaniu y= −1 / 2
i punktu P=(0, 1/2)
naleza do wykresu funkcji f .
Znajdz wzór tej funkcji.
Kompletnie tego nie ogarniam, prosze o wytlumaczenie. Zadanie maturalne.
11 mar 13:17
Daniel: Prosze pomozcie
11 mar 13:37
pigor: .... np. tak : niech
(x,y) ∊ do wykresu szukanej funkcji f , to z warunków
zadania kwadraty odległości tego punktu od danej
prostej i punktu P są równe wtedy i tylko wtedy, gdy
(x−0)
2+(y−
12)
2= y
2 ⇔ x
2+y
2−y+
14= y
2 ⇔ x
2−y+
14=0 ⇔
y = x2+14 − szukany
wzór funkcji
f . ...
11 mar 13:42
Mila: A(x0,y0) − punkt, równodległy od prostej y=−0,5 i punktu P(0;0,5)
Q(x0,−0,5) punkt na prostej
warunek:
|AP|=|AQ|
spróbuj.
Jeśli nie zrobisz, a nikt nie pomoże, to będę na forum po 20.
A leży powyżej prostej.
11 mar 13:49
Daniel: pigor twoje rozwiazanie jest złe
11 mar 14:05
Daniel: |AP|=|AQ|
[0 − x
0 , 0,5−y
0]=[x
0−x
0 , −0,5 −y
0]
x
0=0
0,5−y
0= −0,5−y
0
0,5≠ −0,5
nie umiem , nie wychodzi ...
////
11 mar 14:12
Daniel: Pomoze ktos ? ;<
11 mar 14:34
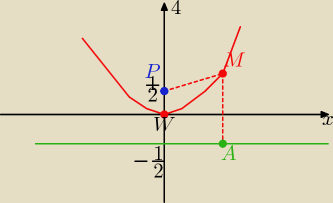
Eta:
| | 1 | | 1 | |
P(0, |
| ) A(x,− |
| ) M(x,y) € f(x) |
| | 2 | | 2 | |
|PM|= |MA| to |PM|
2= |MA|
2
| | 1 | | 1 | |
|PM|2= (x−0)2+(y− |
| )2 = x2+y2−y+ |
| |
| | 2 | | 4 | |
| | 1 | | 1 | |
|MA|2= (x−x)2+(y+ |
| )2 = y2+y+ |
| |
| | 2 | | 4 | |
zatem mamy równość :
| | 1 | | 1 | | 1 | |
x2+y2−y+ |
| = y2+y+ |
| ⇒ x2= 2y ⇒ y= |
| x2 −−−− to parabola |
| | 4 | | 4 | | 2 | |
Odp: zbiór takich punktów M należy do paraboli o równaniu
11 mar 14:49
pigor: ...
o kurcze no jasne, przepraszam, nie dodałem
do y po prawej stronie "mojego" równania |−
12|, a więc jeszcze
raz tak :
(x−0)
2+(y−
12)
2=(y+
12)
2 ⇔ x
2+y
2−y+
14=y
2+y+
14 ⇔
x
2−2y = 0 ⇔ 2y = x
2 ⇔
y=12x2 − szukany
wzór funkcji . ...
11 mar 14:55
Eta:
11 mar 15:01
Daniel: Teraz to sie zgadza
. Dzieki wielkie
11 mar 15:15
Daniel: Eta tylko jeszcze mi powiedz czemu tak
|PM|= |MA| to |PM|2= |MA|2
koniecznie trzeba podosic do kwadratu ?
jesli nie podniesiemy co sie stanie ?
dlaczego tak a nie inaczej ?
11 mar 15:33
Daniel: bo tak robilem , ale nie podnioslem do kwadratu i kicha byla , wiec jakies rady dla mnie
11 mar 15:38
pigor: ... bo odległości to liczby nieujemne, a więc obie te równości są tu równoważne . ...
11 mar 15:43
Daniel: no jo , dobrze pigor , nie wpadlem na to
. Dziekuje ( 2+ ) dla ciebie
11 mar 15:44
pigor: ... , nie podniesiesz to nic się nie stanie, ale co to wtedy za ...
nieciekawy wzór funkcji
f, no i chyba nie dali by ci jednak max. punktów . ...
11 mar 15:46
11 mar 15:50
