obraz odcinka Daniel: Obrazem odcinka AB, gdzie A= (1,0) i , B=( 2,1) w jednokladnosci o skali k>1 i srodku P jest odcinek CD, gdzie C=(4,0), D=(6,2). Zapisz równanie okregu o srodku w punkcie P i promieniu AB. Prosiłbym tylko o rysunek w ktorym miejscu znajduje sie punkt P. Jest to dla mnie nie zrozumiala tresc, takze prosilbym o wyjasnienie czemu tak a nie inaczej . Licze na wasza pomoc. Pozdrawiam Daniel

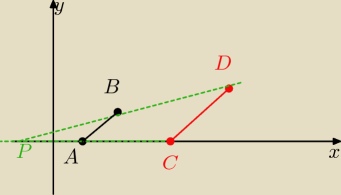
Aga1: Punkt P to punkt przecięcia prostych AC i BD. J_P^k(A)=C , taki , że PC^→=kPA^→

Daniel: Dokladnie tak jak mowisz powinno byc , ale dalej nie rozumiem w ktorej czesci zadania to wynika. Ja to rozumuje w ten sposob ze obraz odcinka w jednokladosci o skali k>1 i srodku P , czyli srodek odcinka CD to punkt P. Kicha , zdaje matme rozszerzona , a nie ogarniam skad to sie bierze . Nie nawidze okregow . Prosze o jakis prosty sposob na wytlumaczenie tego zadania.

Daniel: Jakie to dziwne

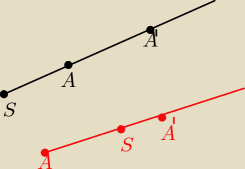
Aga1: S− środek jednokładności, A−dany punkt A^'−− jego obraz 1) punkty S, A i A^' leżą na jednej prostej (zawsze w jednokładności) 2) Jeśli skala jest dodatnia to punkty A i A^' leżą po jednej stronie punktu S. 3) Jeśli k>1, to porządek punktów na prostej jest następujący: S, A, A^' ( rysunek czarny) 4)Jeśli k<0 to S leży pomiędzy A i A^'. (rysunek czerwony). Okręgi − kilka wzorów ( które są w tablicach)

Daniel: Zadanie umiem , tylko najgorzej mi sobie wyobrazic ten punkt P, ciezko wywnioskowac jak dla mnie z zadania gdzie on sie znajduje. Dzieki tobie troche zrozumialem