Logarytm-zbiór punktów Shaya: Zaznacz w układzie współrzędnych zbiór tych punktów (x,y), dla których prawdziwa jest podana równość. Otrzymany zbiór przesuń o wektor v=[−2:1] log_x y=log_y x

Aga1: x>0, y>0,x≠1 , y≠1

	logyy		1
logxy=		=
	logyx		logyx

1
	=logyx,
logyx

log_yx=t

1
	=t
t

t²=1 t=−1 lub t=1 log_yx=−1 lub log_yx=1

	−1
y=		y=x
	x

Mam nadzieję, że dobrze.

Ted:

	1
znasz wzór logab=
	logba

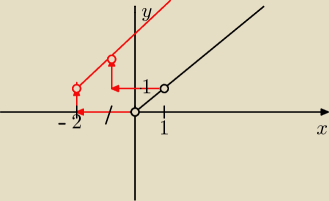
aby zachodziło log_xy=log_yx .... log_xy=log_yx=1 ... ⇒y=x Rysujesz prostą y=x ... i przesuwasz ...

Shaya:

	−1
kk rozumiem ale dlaczego nie narysowałas Aga1 tego wykresu y=
	x

Shaya: aaaaaaaa juz wiem, dziedzina^^

gorki: Prawie dobrze. log_yx=−1 y⁻¹=x

1
	=x
y

	1
y=
	x

I część tej funkcji pasuje do dziedziny.