stereometria
GYT: PILNE! PROSZE O POMOC
Krótsza przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt
60 stopni. Przekątna ściany bocznej ma długosc 4
√10. Oblicz objętosc tego graniastosłupa i
cosinus kata między przekątnymi graniastosłupa, wychodzącymi z jednego wierzchołka.
xData:
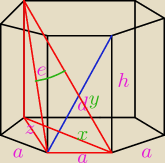
1. Liczę krótszą przekątną (z):
z
2 = a
2 + a
2 − a*a*cos120
o
z
2 = 2a
2 + a
2
z
2 = 3a
2
z = a
√3
2. Uzależniam wysokość (h) graniastosłupa od mniejszej przekątnej podstawy (z):
h = 3a
3, Z tw. Pitagorasa, mając daną długość przekątnej ściany bocznej (d) liczę krawędź podstawy:
h
2 + a
2 = d
2
(3a)
2 + a
2 = (4
√10)
2
9a
2 + a
2 = 160
10a
2 =160
a
2 = 16
a = 4
4. Mając daną krawędź podstawy liczę wysokość graniastosłupa (h):
h = 3a
h = 3*4
h = 12
5. Mając potrzebne dane liczę objętość (V) graniastosłupa:
V = P
p*h
V = 288
√3 [j
3]
6. Z tw. Pitagorasa liczę długość dłuższej przekątnej podstawy (x):
z
2 + a
2 = x
2
3a
2 + a
2 = x
2
4a
2 = x
2
x = 2a
7. Z tw. Pitagorasa liczę długość dłuższej przekątnej graniastosłupa (y):
h
2 + x
2 = y
2
(3a)
2 + 4a
2 = y
2
9a
2 + 4a
2 = y
2
13a
2 = y
2
y = a
√13
y = 4
√13
8. Liczę długość krótszej przekątnej graniastosłupa (e):
e = 8
√3
9. Liczę cosinus kąta (β) zawartego pomiędzy krótszą (e) przekątną graniastosłupa a dłuższą
(y):
a
2 = e
2 + y
2 − 2*e*y*cosβ
4
2 = (8
√3)
2 + (4
√13)
2 −2*8
√3*4
√13*cosβ
16 = 192 + 208 − 64
√39cosβ
− 64
√39cosβ = −384
√39cosβ = 6