sos adaskos: Okrąg o równaniu x² − 6x+ y² −2y +2 = 0 i prosta x+3y+2=0 przecinają się w punktach A,B. Wyznacz długość cięciwy AB tego okręgu.

rumpek: x² − 6x + y² − 2y + 2 = 0 3y = −x − 2 / : 3

	1		2
y = −		x −
	3		3

	1		2		1		2
x2 − 6x + ( −		x −		)2 − 2( −		x −		) + 2 = 0
	3		3		3		3

otrzymasz punkty przecięcia i następnie musisz obliczyć odległość tych punktów korzystając z wzoru: |AB| = √(x_B − x_a)² + (y_B − y_A)² = ..

adaskos: nie bardzo rozumiem

rumpek: rozwiąż równanie które ci napisałem:

	1		2		1		2
x2 − 6x + (−		x −		)2 − 2(−		x −		) + 2 = 0
	3		3		3		3

ponies do potęgi zmień znaki, otrzymasz równanie kwadratowe z które będą dwa x₁ x₂ gotowca nie będzie

Gustlik: x² +y² − 6x −2y +2 = 0 x+3y+2=0 Można prościej niz układem i wzorami skróconego mnozenia, które są najdłuższą metodą wyznaczania środka okręgu i promienia:

	A		−6
a=−		=−		=3
	2		2

	−2
b=−		=1
	2

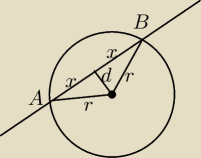
r=√a²+b²−C=√3²+1²−2=√8=2√2 S=(3, 1), r=2√2 Liczę odległość środka okręgu od prostej x+3y+2=0:

	|3+3*1+2|		8		8√10
d=		=		=
	√12+32		√10		10

Liczę x z Pitagorasa: r²=d²+x²

	8
8=(		)2+x2
	√10

8−6,4=x² x²=1,6 x=... dokończ dł. cięciwy=2x=...