Funkcja f jest opisana wzorem f(x)=x^2. Zatem:
Czarna:
a) wartość funkcji dla argumentu 2√2 wynosi 4
b)funkcja f jest rosnąca w zbiorze liczb rzeczywistych
c)zbiorem wartości funkcji f jest zbiór ZWf=(0,+∞)
d)funkcja f przyjmuje wartości dodatnie dla wszystkich argumentów różnych od zera
Bardzo proszę o rozwiązanie
Milo: a) f(2
√2) = (2
√2)
2 = 8 ≠ 4
b) Funkcja f(x) = x
2 nie jest rosnąca, bo np. f(0) < f(−1) (0 < 1)
c) Zbiorem wartości jest <0,
∞), f(0) = 0
d) x
2 ≥ 0 w ℛ, to powszechnie znany fakt (kwadrat liczby rzeczywistej jest nieujemny)
Dlaczego?
1) Jeśli x>0, to x
2 = x*x to iloczyn dwóch liczb dodatnich, więc jest dodatni
2) Jeśli x=0, to x
2 = 0
2 = 0
3) Jeśli x<0, to x
2 = x*x to iloczyn dwóch liczb ujemnych, więc też jest dodatni (dwa minusy
dają plus czy coś
)
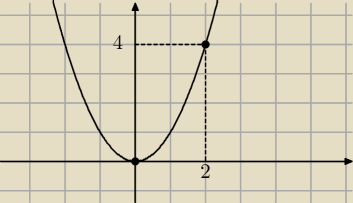TO jest wykres y=x2
Patrz i analizuj wszystkie podpunkty po kolei