Środkowe w trójkącie równoramiennym triangle: Wykaż, że jeśli dwie środkowe trójkąta mają równe długości, to trójkąt ten jest równoramienny.

ola:

pigor: ..., niech ΔABC dowolny i w nim AD=BE − równej długości środkowe boków BC i AC odpowiednio, przecinające się w punkcie S, to stąd i tw. o środkowych AS=BS, zatem |∡BAS|= |∡ABS| jako katy Δ równoramiennego ABS, czyli tym samym |∡BAD|= |∡ABE|, stąd ΔABD = ΔBAE − ΔΔ przystające (2 boki kąt między nimi równe), więc α= β kąty przy wierzchołkach A i B odpowiednio równe, czyli AC=BC − ΔABC − równoramienny c.n.w.

wredulus_pospolitus:

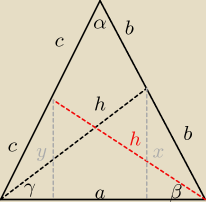
	1		1
PABC =		*2c*b*sinα +		a*x
	2		2

oraz

	1		1
PABC =		*c*2b*sinα +		a*y
	2		2

czyli:

1		1		1		1
	*2c*b*sinα +		a*x =		*c*2b*sinα +		a*y −> x=y
2		2		2		2

dolne trójkąty są przystające (bo kąty β i γ są równe −−− funkcje trygonometryczne się kłaniają) czyli b=c c.n.w.

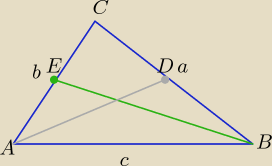
Eta: Trójkąt o bokach a, b, c >0

	1
|AD|=		√2b2+2c2−a2
	2

	1
|BE|=		√2a2+2c2−b2
	2

|AD|=|BE| ⇒ 2b²+2c²−a²=2a²+2c²−b² ⇒ 3a²=3b² ⇒ a=b zatem trójkąt jest równoramienny