z tom: Znajdź zbiór środków wszystkich okręgów przechodzących przez punkt P(3,2) i stycznych do osi OX.

rumpek: ogólny wzór (x − a)² + (y − b)² = r², skoro ma być styczny do osi O_x, czyli musi spełniać warunek: (x − a)² + (y − r)² = |r|² (|r|² = (√r²)² = r² ) (x − a)² + (y − r)² = r² (3 − a)² + (2 − r)² = r² 9 − 6a + a² + 4 − 4r + r² = r² 13 − 6a + a² = 4r / : r

	1		3		13
r =		a2 −		a +
	4		2		4

Zatem zbiorem środków jest parabola

tom: Dziękuję

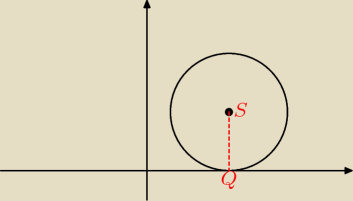
Basia: S(a,b) ⇒ okrąg przechodzi także przez punkt Q(a,0) a r=b b musi być >0, bo okrąg przechodzi też przez punkt P(3,2) mamy więc (x−a)²+(y−b)² = b² stąd: (3−a)² + (2−b)² = b² 9 − 6a + a² + 4 − 4b + b² − b² = 0 a² − 6a + 13 = 4b /:4 b = ¹₄a² − ³₂a + ¹³₄ czyli parabola y = ¹₄x² − ³₂x + ¹³₄