: :): Dla jakich wartości parametru a jeden z pierwiastków równania (2a+1)x²−ax+a−2=0 jest większy od 1, a drugi mniejszy od 1?

AC: (2a+1)f(1)<0⇒ (2a−1)(2a+1)<0 ⇒ a∊(−1/2; 1/2)

:): Można by troszkę słownie powiedzieć o co tu chodzi? bo chyba zawieche mam...

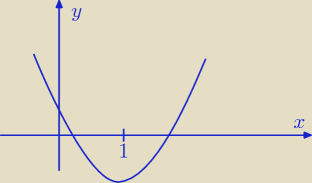
Godzio: Dla 2a + 1 > 0 mamy f(1) < 0 Dla 2a + 1 < 0 mamy f(1) > 0 Sprowadzając to do jednego przypadku mamy: (2a + 1) * f(1) < 0 A do tego: Δ > 0 Znajdź rozwiązanie takiego układu:

⎧	(2a + 1) * f(1) < 0
⎩	Δ > 0

:): A no właśnie... Chwilowa blokada. Dziękuję

pigor: ... a słownie − jak pytała(e)ś − taki układ oznacza , że Δ >0 − muszą istnieć 2 różne pierwiastki , a (2a+1) * f(1)< 0 − współczynnik przy x² i wartość trójmianu w x=1 są różnych znaków