fail :X Kasia: Dla supermozga Wysokosc ostroslupa prawidlowego trojkatnego tworzy z krawedzia boczna tego ostroslupa kat x, taki ze cosx=0,8. Krawedz podstawy ma dlugosc 3. Oblicz pole powierzchni calkowitej tego ostroslupa.

Artur z miasta Neptuna: cosx = 0.8 ⇔ sin x = √1−0.64 = √0.36 = 0.6

	1/3hp
sin x =		.... gdzie hp = wysokość podstawy, czyli trójkąta równobocznego o
	hb

boku 3 h_b = wysokość ściany bocznej

	a√3		3√3
hp =		=
	2		2

hp		√3
	=
3		2

	3		√3/2		5√3
sin x =		=		⇔ 3hb = 5√3 ⇔ hb =
	5		hb		3

P_c = P_p + 3*P_b = ....

Kasia: jak moglbys obliczyc dokladna wartosc bede wdzieczny bo widze ze juz cos jest zle, bo ja mam krawedz boczna 5√3 /4

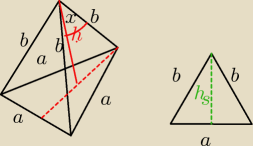ewa: h−wysokość ostrosłupa h_p− wysokość Δ równobocznego w podstawie a=3 krawędź podstawy

	0,6		3
cosx=0,8 ⇒ sinx=√1−0,64=0,6 ⇒tgx=		=
	0,8		4

	a√3		3√3
hp=		=
	2		2

2   hp 3
	=tgx
h

2   3√3   * 3   2		3
	=
h		4

	4√3
h=
	3

	a2√3		9√3
Pp=		=
	4		4

h		4√3		10		5√3
	=cosx=0,8 → b=		*		=
b		3		8		3

h_s²=b²−(0,5a)²

	25		9		73
hs2=		−		=
	3		4		12

	73		√73		√219
hs=√		=		=
	12		2√3		6

	1		√219		3√219
Pb=3*		*3*		=
	2		6		4

	3√219		9√3		9√3+3√219
Pc=		+		=
	4		4		4

ewa: Ale x to kąt między wysokością ostrosłupa a krawędzią boczną, a nie pomiędzy wysokościa ostrosłupa a wysokością ściany bocznej!

Kasia: czyli ewa dziekuje , dobrze mam