a Karolaa: f(x) = ln (x²−3/x²−1) * / (podzielic) x=1, x=−1 ale wyrzucamy je bo x≠1 x≠−1 Wiec jaka jest dziedzina?

pigor: ... D_f opisuje ... wystarczająco taka nierówność :

x2−3
	>0 ⇒ (x−√3)(x+√3)(x−1)(x+1) >0 ⇔ x<−√3 lub −1< x <1 lub x >√3 ⇔
x2−1

x ∊ (−∞;−√3) U (−1;1) U (√3;+∞)=D_f − szukana dziedzina danej funkcji . ...

Karolaa: FAKTYCZNIE! WIELKIE DZIEKI!

Karolaa: D: (−∞;−√3) (√3;+∞)

Karolaa: ?

Karolaa: Acha i jesli na samym poczatku zapisuje Df: R / {−1,1} To potem pisze ta druga dziedzine i to jest dobrze? tak moze byc ze dwie dziedziny?

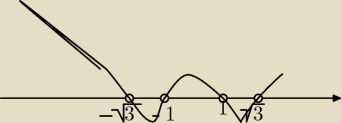
krystek: I masz ilustrację.

Karolaa: i od <−1;1> Wyrzucam! tak? czyli dziedzina (−∞;−√3) (√3;+∞)

Aga1: Dziedzina taka, jak napisał pigor

Karolaa: (−∞;−√3) ( −1;1) (√3;+∞)

Tragos: D:

	x2 − 3
{		> 0
	x2 − 1

{ x² − 1 ≠ 0 { x ∊ (−∞, −√3) u (−1, 1) u (√3, +∞) { x ≠ 1 i x ≠ −1 x ∊ (−∞, −√3) u (−1, 1) u (√3, +∞) D = (−∞, −√3) u (−1, 1) u (√3, +∞)

Karolaa: MMH DZIEKUJE!

krystek: Dlaczego wyrzucasz masz mieć wartości dodatnie −nad osią . Popatrz jak napisał Pigor−masz odpowiedź Ja daje graficzny obraz rozwiązania tej nierówności.

Aga1: Tak, tylko połącz znakiem U