Zadanie Aga: proszę o pomoc Mikołaj który stoi wieczorem 3m od latarni rzuca cień o długości 1m.Mikołaj ma 1,6m wzrostu. Ile wynosi wysokość latarni?

xpt: wysokość latarni oznaczona jako x Ta przerywana koślawa linia to linia padania światła latarnii (wybacz, że taka krzywa, ale jakoś jeszcze się nei przyzwyczaiłem do możliwośći rysowania tutaj ) z twierdzenia talesa musisz ułożyć proporcję,

długość cienia		1m
	=
wysokość mikołaja		1,6m

Teraz musisz ułożyć 2gie równanie, żeby otrzymać w mianowniku x. Zastanów sie jak to zrobić i napisz mi co wymyśliłaś

tim: RYSUNEK? Chyba się nie pojawił...

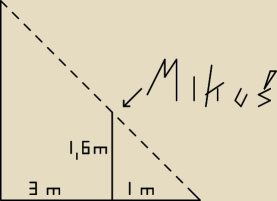
xpt: Dodałem rysunek, jeszcze raz po poprzedni się nie wyświetla.

xpt: ups − zapomniałem oznaczyć latarni jako "x", ale latarnia to ta duża pionowa kreska po lewej mikołaja oznaczyłem "Mikuś", ale tego pewnie można się domyślić

Aga: wysokość latarni wyszła mi 4,8m −dobrze

swietlik: Po obliczeniach "w głowie" wyszło mi 6,4 m. W Twoich obliczeniach jest błąd − zamiast 3m powinnaś podstawić 4m (odl. mikolaja od lat. + dł.cienia) A oto inne roziązanie: Zauważ, że duży trójkąt i mały mają wspólny kąt − nazwijmy go α. Najprościej jest to chyba zrobić z funkcji trygonometrycznej tj.

	wyskość mikołaja
1 rownanie tgα=
	długość cienia

	wysokość latarni (x)
2 rownanie to tgα=
	odległość mikołaja od latarni + cień mikołaja

I teraz wystarczy porównać równania po czym wyliczyć X Jeżeli nie miałaś f.tryg. to przepraszam za zamieszanie

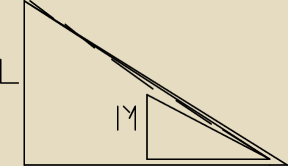
tim: Prościej mówiąc korzystamy z proporcji dwóch trójkątów. Wyżej.