Twierdzenie sinusów i cosinusów Nikita: Niech ABC bedzie dowolnym, trójkątem . Oblicz stosunek

	s12 + s22 + s32
	a2 + b2 + c2

gdzie a,b,c są długościami boków, s₁, s₂, s₃ zaś długościami środkowych tego trójkąta.

Godzio: Masz wzory na środkowe, które nietrudno wyprowadzić z tw. cosinusów http://pl.wikipedia.org/wiki/%C5%9Arodkowa_tr%C3%B3jk%C4%85ta

Nikita: niby jak je wyprowadzic z tego twierdzenia?

Godzio:

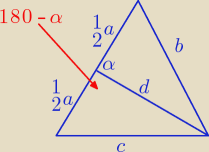
	1		1
b2 =		a2 + d2 − 2 *		adcosα
	4		2

	1		1
c2 =		a2 + d2 − 2 *		accos(180 − α)
	4		2

cos(180 − α) = −cosα Zatem:

	1		4b2 − a2 − 4d2
b2 =		a2 + d2 − abcosα ⇒ cosα =
	4		4ab

	1		4b2 − a2 − 4d2
c2 =		a2 + d2 + ac *
	4		4ab

No i teraz zwykłe przekształcenia

Nikita: to znaczy jakie?

Nikita: