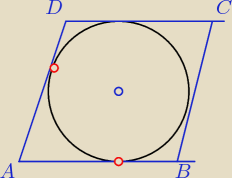
GEOMETRIA ANALITYCZNA Ania: Okrąg o równaniu (x−7)² + (y−1)²=20 jest wpisany w romb ABCD. Okrąg ten jest styczny do boku

	3		4
AB w punkcie S1=(9,−3) i styczny do boku AD w S2=(2		, 1		).
	5		5

Znajdź współrzędne A, B, C, D.

Ted: Środek okręgu S=(7, 1)

	−3−1
Prosta przechodząca przez S i S1 m: y−1=		(x−7) ... ⇒ y=−2x+15
	9−7

Prosta zawierająca bok AB przechodzi przez S₁ i ma współczynnik kierunkowy a=1/2 więc n: y+3=1/2(x−9) ... ⇒ y=1/2x−7,5 Identycznie wyznaczysz prostą zawierającą bok AD ... a potem wpółrzędne punktu A (punkt przecięcia się prostych) ... itd −

Jolanta: proste mają a₁*a₂=−1 jeżeli są prostopadłe. prosta przechodzaca przez środek i S₁ ma a=−2 ale nie mozemy zakładac ,ze prosta zawierajaca

	1
bok AB jest do niej prostopadła czyli nie wiemy czy a=
	2

Jolanta: Wypraszam sobie głupie zarty.Oczywiście ,ze są prostopadłe