Pole koła, pole wycinka koła helpme: Odległość środków dwóch kół o jednakowych promieniach długości r jest równa r. Oblicz pole części wspólnej tych kół.

	4 π − 3 √3
Wynik powinien wynieść		r2
	6

Wskazówka: Niech O₁ i O₂ będą środkami kół, A jednym z ich punktów wspólnych. Zauważ, że trójkąt O₁O₂A jest równoboczny. Bardzo proszę o rozwiązanie i wyjaśnienie co z czego wynika, z jakich wzorów należy skorzystać.

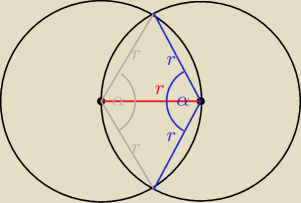Artur z miasta Neptuna: α = 120^o Obliczasz pole wycinka okręgu ograniczone szarymi odcinkami. Kąt pomiędzy nimi to 120^o ... czyli P_wycinka = ¹/₃ P_koła Tak samo z odcinkami niebieskimi. Należy teraz odjąć pole części wspólnej tych wycinków kół ... są nimi dwa trójkąty równoboczne, o boku równy r. tak więc:

	r2√3
Pszukane = 1/3 Pkoła + 1/3 Pkoła − 2Ptrójkąta = 2/3 * πr2 − 2		=
	4

	4πr2 − 3√3r2		4π − 3√3
=		=		* r2
	6		6

Aga1: P_o−−−pole odcinka koła P_o=P_{wycinka koła}−P_ASB α=120⁰, bo trójkąty S S₁A i SS₁B są równoboczne o boku długości r. P_f=2*P_o

	1
P{trójkąta		r2*sinα
	2

	α
Pw=		*πr2
	3600

podstaw do wzoru i dokończ.

helpme: Super, dziękuję

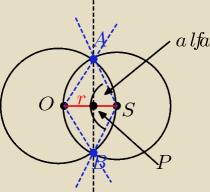ejendi: AB=l wycinek(AS) Δ(ASP) Pwycinka=πr²*α/2π=αr²/2 cos(α/2)=r/2r=1/2 α/2=π/3⇒α=2π/3 Pwycinka=πr²/6 PΔ=l/2*r/2*1/2 1 l/2=√r² − r²/4=r√3/2 PΔ=r²√3/6 P=4(Pwycinka−PΔ)

	2
P=4(πr2/6−r2√3/6)=		r2(π−√3)
	3

taki wynik, nie mogę znaleść błędu

Artur z miasta Neptuna: ejendi ... P=4(Pwycinka−PΔ) ... czemu 4P_Δ, a nie 2P_Δ

Artur z miasta Neptuna: ooo ja pitolę ... po co tak podzielone

	r2√3
dobra ... PΔ powinien wyjśc		... w końcu 2*2*2 = 8 a nie 6
	8

ejendi: racja nowy wynik mi wyszedł √6=2

ejendi: ³√6=2

Artur z miasta Neptuna: normalnie geniusz