przekształcenia płaszczyzny Przemek: Niestety nie było mnie na kilku lekcjach i nie wiem wogóle jak zabrać się za takie zadania. Dana jest prosta k o równaniu y=2x −3. Znajdź równanie prostej m będącej obrazem prostej k o przekszałceniu: T[−³₂, 0]. Poprosiłbym o wytłumaczenie krok po kroku i dlaczego tak jest. Serdecznie dziękuje

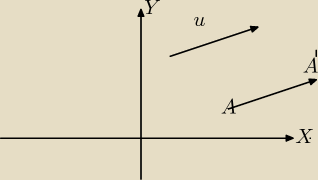
Aga1: Obrazem punktu A(x,y) w przesunięciu równoległym o wektor u^→= [a,b] jest punkt A^'(x^', y^') taki , że x^'=x+a, y^"=y+b. u^→=AA^'→

Przemek: Znam tą teorie z podręcznika, ale wogóle nie wiem jak to zastosować w praktyce. Poprosiłbym Cie o rozwiązanie tego przykładu krok po kroku, bardzo mi zależy. Z góry dziękuje.

Aga1: Zadanie można zrobić graficznie. Wektor przesunięcia T[−3/2,0] Do prostej y=2x−3 należą punkty A=(0,−3), punkt A^'=(0−3/2, −3+0]=[−3/2,−3] B=(1,−1), B^'=(−1/2,−4)Zaznaczasz punkty A i B rysujesz daną prostą. Zaznaczasz A^', B^' rysujesz drugą prostą. Zauważ, że te proste są równoległe. Równanie prostej A^'B^' możesz napisać znanymi Ci sposobami. Lub wykorzystać własność. Po przesunięciu wykresu funkcji y=f(x)o wektor [p,q] otrzymujemy wykres funkcji y=f(x−p)+q Tu p=−3/2, a q=0. x−p=x+3/2 Do wzoru zamiast x wstawiasz (x+3/2) y=2(x+3/2)+0 y=2x+3

Przemek: Jeszcze jedno pytanie, pewnie głupie i oczywiste. Skąd wzięły się punkty A i B?

Aga1: Obliczyłam, nie wiem jak dotychczas liczyłeś, Za x podstawiłam 0 i obliczyłam y Gdy x=0, to y=2*0−3=−3 , ⇒ (0,−3) Gdy x=1, to y=2*1−3=−1⇒ (1,−1)