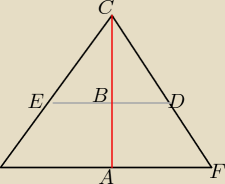
planimetria - jedno twierdzenie mówi to, inne co innego matroz: mamy sobie trójkąt równoboczny o dł. boku 6 Mamy obliczyć długość odcinka przechodzącego przez środek ciężkości trójkąta (na rys. oznaczyłem siwym kolorem). 1. Obliczyłem korzystając z twierdzenia mówiącego, że odcinek łączący środki dwóch boków

	6
trójkąta jest równy połowie długości trzeciego, czyli x=		=3
	2

2. Obliczyłem korzystając z tego, że wys. trójkąta równobocznego dzielą sie w stosunku 1:2 wysokość oznaczyłem czerwonym kolorem |ED|=x

	x
|BD|=
	2

	2		2		6√3
|BC|=		h=		*		=2√3
	3		3		2

|CB|BD|=|CA|AF|

2√3		3√3
	=
0,5x		3

x=4 Jaki zrobiłem błąd? Wiem że wynik to 4, ale co z pierwszą opcją? Proszę o szybką odp, jutro piszę próbną maturę pozdro

Beti: W 1. i 2. liczysz dwie różne rzeczy, bo: 1. Skoro B i D to środki boków trójkąta, to B też jest śodkiem wysokości i AB jest

	1
		h
	2

	1
2. Skoro ED przechodzi przez środek ciężkości, to AB jest		h
	3

matroz: Czemu B jest środkiem wysokości

Krl: Z podobieństwa trójkątów na przykład.

Beti:

matroz: co do 1. , co z tym twierdzeniem (odcinek łączący środki dwóch boków trójkąta jest równy połowie długości trzeciego) dlaczego tutaj nie wyszło?

Mila: |ED|=6:2=3 i co Ci nie zgadza?

matroz: bo ma wyjść 4, to fragment zad. z próbnej matury z rozszerzenia

matroz: Treść tego zadania: Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy a=6 i wysokości h=9. Oblicz pole powierzchni przekroju tego graniastosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek ciężkości drugiej podstawy. chodziło mi cały czas tylko o ten bok |ED| który jest potrzebny do obliczenia, dalej potrafię rozwiązać

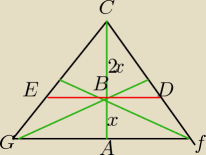
Mila: Zaraz, jeśli to odcinek lączący środki boków Δ to 3. Jeśli to odcinek przechodzący przez środek ciężkości, to 4 , dlatego, że :

CB		ED		2x		ED
	=		⇔		=
CA		GF		3x		6

Twój rysunek nie pasuje. ED=4cm

matroz: @Mila: no tak, rozumiem swoją pomyłkę. Tylko proszę o wytłumaczenie Twoich proporcji:

CB		ED		2x		ED
	=		⇔		=
CA		GF		3x		6

To z 2x i 3x rozumiem, bo środkowe dzielą się w stosunku 1:2

	ED
ale czemu to przyrównać do		? jakie twierdzenie wykorzystałaś?
	GF

matroz: można to ew. z Talesa

CB		CA
	=
BD		AF

Mila: Z podobieństwa ΔCED i ΔCGF. Twoja proporcja też dobra.