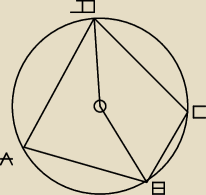
Wyznacz miary kątów w czworokącie wpisanym w okrąg. xaxa: Witam, Proszę o pomoc w rozwiązaniu, a w zasadzie to o sprawdzenie czy dobrze policzyłem to zadanie. Punkt O jest srodkiem okregu. Miara ADC jest rowna 55. Miara DOB jest rowna 150. Wyznacz miary pozostalych katow czworokata ABCD. Według moich obliczeń kąty wynoszą: DOB = 150 i po drugiej stronie 210 DCB i DAB jako wpisane na tym samym łuku = 75 ODC = 45 jako wpisany oparty na promieniu ADO = 10 jako ADC rowny 55 − ODC rowny 45 OBC = 90 jako 360 − 150 (DOB) − 75 (DCB) − 45 (ODC) ABO = 65 jako 360 − 10 (ADO) − 210 − 75 (DAB) Z góry dzięki za sprawdzenie i poprawę ewentualnych błędów.

Beti: jeśli czworokat jest wpisany w okrąg to sumy przeciwległych kątów są = 180^o Skoro więc ADC = 55^o, to ABC = 180−55 = 125^o Skoro BOD = 150^o, to BAD = 1/2*150 = 75^o oraz BCD = 180−75 = 105^o