W trapezie ABCD, AB II DC, przekątne przecinają się w punkcie E. Wiedząc, że IAB

W trapezie ABCD, AB II DC, przekątne przecinają się w punkcie E. Wiedząc, że IAB Karol: W trapezie ABCD, AB II DC, przekątne przecinają się w punkcie E. Wiedząc, że IABI = 3IDCI oraz pole trapezu jest równe 64 cm2, oblicz pole trójkąta AED.

6 mar 20:40

Karol: pomoże ktoś?

6 mar 20:48

Grander: siema masz tutaj to zadanie https://matematykaszkolna.pl/forum/129002.html

6 mar 20:50

Karol: ale ono jest zle rozwiązne.

6 mar 20:52

Eta:

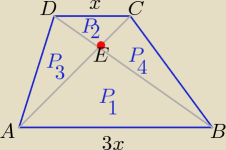
x>0 |AB|=3x |CD|=x P₃=P₄= P(ΔAED)

	3x
ΔABE ~ ΔDCE w skali k=		= 3
	x

	P₁
to:		= k²= 9 ⇒ P₁= 9P₂ oraz P₃= P₄= k*P₂ = 3P₂
	P₂

P_tr= P₁+2P₃+P₂ =64 ⇒ 9P₂+6P₂+P₂= 64 ⇒ P₂= 4 to: P₃= 3*4 = P(ΔAED)= 12

6 mar 21:13

Karol: a skad wiemy,ze P3=p4? i skad to sie wzielo? k*P2 = 3P2

6 mar 21:24

Mila: P_ΔDCB=1/2 x*h P_DCA=1/2x*h czy teraz jasne?

6 mar 21:47

Karol: jasne! a skad jest k*P2?

6 mar 21:51

Mila: ΔDEC iΔCEB mają tę samą wysokość zatem pole ΔCEB jest tyle razy większe ile razy jest wieksza jego podstawa, czyli 3 razy bo EB=3 *DE.

6 mar 22:05