wyznacz współrzędne punktu przecięcia się przekątnych kwadratu ABCD jeżeli; iga: wyznacz współrzędne punktu przecięcia się przekątnych kwadratu ABCD jeżeli; A=4,0 B=2,4 C=−2,2 D=0,−2 mi wyszło S=1,1

Karola: POTRZEBUJE POMOCY! Wyznacz A∪B, A∩B jezeli A=<−3,4> B=(3,∞)

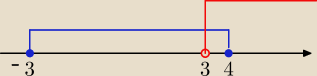
Basia: teraz pomyśl

Janek191: A = < − 3 ; 4 > B = ( 3 ; + ∞ ) więc A ∪ B = < − 3 ; + ∞ ) A ∩ B = ( 3 ; 4 >

Karola: Wyznacz A\B, B\A jezeli A=<−3,4> B=(3,∞) Bede wdzięczna i z gory dziękuje

Gustlik: Basiu, Janek191 i pozostali Forumowicze mam propozycję co do rysowania − lepiej rysować metodą Bogdana. Wtedy widać, czy końce należą do przedziału i nie robi się błędów. Ta szkolna metoda to metoda "Samych swoich". To wygląda tak, jakby Kargul posadził drzewo na płocie graniczącym z Pawlakiem, pół drzewa jest u Kargula, a drugie pół u Pawlaka, a potem się żrą między sobą, czyje to drzewo. I tak samo jest z tymi kropkami − nie wiadomo, czy należą do przedziału, czy nie. A tak widać, że A∩B=(3, 4>.

Gustlik: iga robisz tak − wyznaczasz równania prostych AC i BD i układem równań tych prostych znajdujesz punkt przecięcia: A=(4,0) B=(2,4) C=(−2,2) D=(0,−2) Najlepiej z wektorów, bo współczynnik kierunkowy można obliczyć ze współrzędnych wektorów:

	wy
a=		, gdzie [wx, wy] to współrzędne wektora wyznaczającego prostą.
	wx

U nas to będą wektory AC^→ i BD^→ AC^→=[−2−4, 2−0]=[−6, 2]

	2		1
a=		=−
	−6		3

	1
y=−		x+b
	3

Wstawiamy współrzędne A lub C i mamy równanie, np. A:

	1
0=−		*4+b
	3

4
	=b
3

	4
b=
	3

	1		4
y=−		x+
	3		3

Tak samo z prostą BD: liczymy wektor BD^→ BD^→[0−2, −2−4]=[−2, −6]

	−6
a=		=3
	−2

y=3x+b Wstawiamy współrzędne B lub D, np. D=(0,−2) −2=3*0+b b=−2 y=3x−2 Teraz rozwiazujemy układ:

	1		4
{ y=−		x+		(1)
	3		3

{ y=3x−2 (2)

	1		4
−		x+		=3x−2 /*3, żeby pozbyć się ułamków
	3		3

−x+4=9x−6 −10x=−10 /:(−10) x=1 Wstawiamy to do któregoś z rownań, najlepiej do (2), bo nie ma ułamków i się łatwiej liczy: y=3*1−2 y=1 Rozwiązanie: { x=1 { y=1 Zatem punkt przeciecia przekątnych kwadratu ma współrzędne (1, 1)

5-latek: Chociaz to zadanie jest z 2012r to zeby policzyc punkt przeciecia sie przekatnch w kwadracie to nalezy policzyc wsplrzedne srodka jednej z p;rzekatnych wykorzystujac fakt ze w kwadracie przekatne przecinaja sie w srodku tak samo jak w postokacie czy rombie >

Gustlik: 5−latek, masz rację będzie szybciej.

Janek191: A = ( 4; 0) B = ( 2; 4) C = ( − 2; 2) D = ( 0; − 2) Przekątne kwadratu przecinają się w punkcie , który jest ich wspólnym środkiem, więc S = środek AC lub S − środek BD

	4 − 2		0 + 2
S = (		;		) = ( 1; 1)
	2		2

lub

	2 + 0		4 − 2
S = (		;		) = ( 1; 1)
	2		2

Zadanie z 6 III 2012 r.

Karola: Wyznacz A\B, B\A jezeli A=<−3,4> B=(3,∞)

Technik: Gustlik a ja robię tak jak Basia i dla mnie jest to najlepsza metoda i nie mam zamiaru jej zmieniać

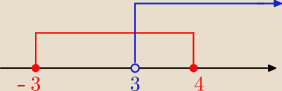
Technik: A\B=<−3,3> B\A=(4,∞)

Gustlik: Tak, tylko zamalowana kropka jest automatycznie brana przez uczniów jako przedział domknięty, a niezamalowana − jako otwarty. Jest to bardzo NIEPRZEJRZYSTA I NIEBEZPIECZNA METODA. Większość uczniów zrobi tak: A\B=<−3, 3) B\A=<4, +∞) To powszechny i często spotykany błąd przy stosowaniu tej metody. Rysując przedziały metodą Bogdana tego błędu uczeń nie popełni − wiem to z własnego doświadczenia. Odkąd zacząłem stosować tę metodę, moi uczniowie przestali popełniać ten błąd. Z rysunku wyraźnie widać, że A\B=<−3, 3>, a B\A=(4, +∞) Szkoda, że tu nie ma na forum dzisiaj Bogdana, on by to potwierdził. Opis metody Bogdana jest tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3408 oraz tutaj: https://matematykaszkolna.pl/forum/53855.html .