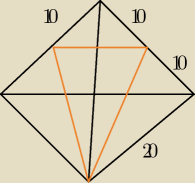
Pole przekroju ostrosłupa prawidłowego MatDylemat: Oblicz pole zaznaczonego przekroju ostrosłupa prawidłowego. Proszę o pomoc w wyliczeniu tego zadania, bo nie mam pojęcia jak się za to zabrać. Nie wiem, czy dobrze myślę, ale wydaje mi się, że nie ma dowodu na to aby podstawa przekroju była linią środkową... Z góry dziękuję za objaśnienia

Aga1: Podstawa tego trójkąta łączy środki krawędzi? zapisz treść zadania.

MatDylemat: Właśnie nie jest wspomniane, dlatego proszę o pomoc. Treść jak wyżej: Oblicz pole zaznaczonego przekroju ostrosłupa prawidłowego.

Aga1: Czy to jest czworościan foremny o krawędzi długości a=20? Jeśli tak, to podstawa trójkąta jest równa 10, a ramię trójkąta jest równe wysokości trójkąta

	a√3
równobocznego b=		=10√3.
	2

h trójkąta wyliczysz z twierdzenia Pitagorasa h²=(10√3)²−5²

MatDylemat: To było pierwsze rozwiązanie, które przeszło mi przez myśl, jednak nie jest wspomniane, że to czworościan foremny, a nie potrafię tego dowieść. Z powyższego pole wychodzi 25√2. Prawidłowa odpowiedź ponoć jest: 2√11

Aga1: h²=300−25=275 h=√275=5√11

	1
P=		*10*5√11=25√11
	2

MatDylemat: Tak banalne obliczenia to oczywiście potrafię, jak zresztą wszystkie powyższe. Problem jest w tym, żeby wykazać, że to czworościan foremny, a jeśli nie to znaleźć alternatywną metodę liczenia. Mimo wszystko oczywiście dziękuję za chęci i liczę na pomoc w zadaniu. Pozdrawiam!