Proszę o pomoc matematyk: napisz rownanie wspoplnych stycznych do okregów x²+y²=1 i (x−4)² +y²=1

M:

M:

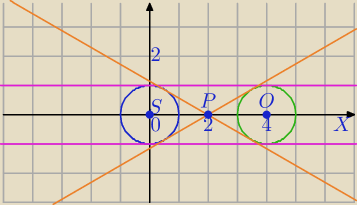
Mila: 1) y=1, y=−1 − styczne (zewnętrzne) 2) r₁=r₂=1 Styczne wewnętrzne: s: y=ax+b i (2,0)∊s 0=2a+b,b=−2a, y=ax−2a⇔ s: ax−y−2a=0 Odległość punktu O=(0,0) od stycznej jest równa r=1.

|a*0−0−2a|
	=1
√a2+1

2|a|=√a²+1

	1		1
stąd a=		lub a=−
	√3		√3

Równania stycznych (wewnętrznych):

	1		2		1		2
y=		x−		lub y=−		x+
	√3		√3		√3		√3

II sposób geometryczny (?) Potęga punktu P względem okręgów jest równa p²=|PS|²−r²=3 Przecięcie okręgów: (x−2)²+y²=3 i x²+y²=1 stąd punkty styczności Q₁ i Q₂

	1		√3		1		√3
Q1=(		,		) i (2,0) oraz Q2=(		,−		) i (2,0)
	2		2		2		2

s: y=ax+b i podane punkty wyznaczają szukane styczne Trudności w niektórych zadaniach przy II sposobie mogą wynikać ze zbyt "brzydkich" punktów styczności. Próbować trzeba.

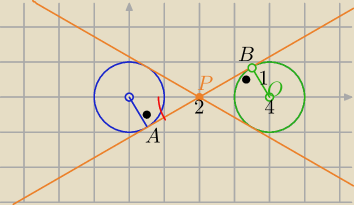Jaga: 3 sposób : wΔPOB : |PB|= √4−1=√3 tgα= a⇒ a=1/√3a lub a= −1/√3 styczne mają równania ( bez wyznaczania współrzędnych B i A s: y=ax+b lub s: y= −ax+b P(2,0)

	1		2		1		2
s : y= −		x+		lub s: y=		x−
	√3		√3		√3		√3

Mila: