Tożsamość czworokąta Marek19: Proszę o dowód tej tożsamości . Znalazłem ją jako tożsamość dla dowolnego czworokąta i chciałbym wiedzieć jak to się dowodzi: a²+b²+c²+d²=e²+f²+4x² gdzie: a,b c,d , − boki dowolnego czworokąta e,f − przkątne x− odległość pomiędzy środkami przekątnych

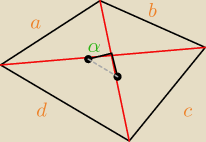
Artur z miasta Neptuna: z' −−− o ile została wydłużona część przekątnej (ponad połowę długości całej przekątnej) e w' −−− analogicznie dla przekątnej f

	e		f
dla uproszczenia zapisu − z =		; w =
	2		2

zakładam, że: środki przekątnych są w zaznaczonych kropkami miejscach z tw. cosinusów 'jedziesz': a² = (z+z')² + (w−w')² − 2((z+z')(w−w'))cos α b² = (z−z')² + (w−w')² − 2((z−z')(w−w'))cos (180−α) c² = (z−z')² + (w+w')² − 2((z−z')(w+w'))cos α d² = (z+z')² + (w+w')² − 2((z+z')(w+w'))cos (180−α) ________________________________________+ L =a²+b²+c²+d² P = 2((z+z')² + (z−z')² + (w+w')² + (w−w')²) − 2cosα((z+z')(w−w') − (z−z')(w−w') + (z−z')(w+w') − (z+z')(w+w')) = = 2(2z² + 2z'² + 2w² + 2w'²) − 2cosα[(w−w')(2z') − (w+w')(2z')] = = (4z² + 4w²) + 4z'² + 4w'² − 2cosα[2z'*(−2w')] = (4z² + 4w²) + 4(z'² + w'² + 2z'w'cosα) = = (4z² + 4w²) + 4(z'² + w'² − 2z'w'cos(180−α)) = // tw. cosinusów w drugą stronę // =

	e		f
= 4z2 + 4w2 + 4x2 = 4* (		)2 + 4* (		)2 + 4x2 = e2 + f2 + 4x2
	2		2

c.n.d.