ównanie stycznych okręgu adam78: Napisz równania stycznych do okręgu o środku w punkcie S = (−1,1) i promieniu r = pierwiastek z 5 poprowadzonych z punktu A = (2,0) .

elpe: równanie okręgu (x+1)²+(y−1)²=5 A(2,0) zatem y=ax+b ald pkt a bd 0=2a+b →b= −2a zatem y=2ax−2a odległość pkt od prostej=r

ejendi: równanie prostej przez A(2,0): y−0=a(x−2); y=ax−2a

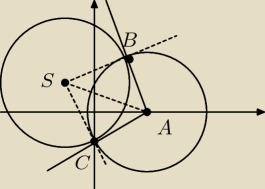
ejendi: S = (−1,1); A = (2,0) SB=√5 SA²=(2+1)²+(0−1)²=10 AB²=SA²−SB²=5 okrąg S: (x+1)²+(y−1)²=5 okrąg A: (x−2)²+(y−0)²=5 punkty przecięcia S: i A: x²+2x+1+y²−2y+1=x²−4x+4+y² 2x+4x−2y+2−4=0 6x−2y−2=0 y=3x−1 to do równania A: x²−4x+4+9x²−6x+1=5 10x²−10x=0 x²−1=0⇒x(x−1)=0⇒x1=0; x2=1 y1=−1; y2=2⇒B(1,2); C=(0,−1) styczne przez AB i AC