zad megi: Dane są punkty które leżą na okręgu , oblicz promień tego okręgu A=(3,4) B(0,3) C(1,0)

M:

Bo_ra: Równanie okręgu o środku S=(a,b) i promieniu (r) ma pstac x²+y²−2ax−2by+a²+b²−r²=0 Oznaczmy c=a²+b²−r² Wtedy równanie to bedzie miało postac x²+y²−2ax−2by+c=0 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− A=(3,4) B=(0,3) C=(1,0) Punkty te musza spełniać to równanie {9+16−6a−8b+c=0 {0+9−0a −6b+c=0 {1+0−2a−0b+c=0 {−6a−8b+c=−25 { −6b+c=−9 {−2a +c=−1 a=2 b=2 c=3 a²+b²−r²=3 4+4−r²=3 −r²=−5 r²=5 r=√5

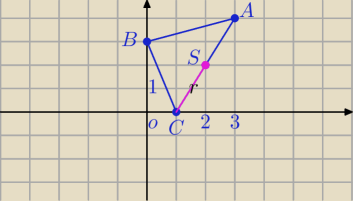
Mila: A=(3,4), B(0,3) ,C(1,0) ) BA^→=[3,1], BC^→=[−1,−3] BA⊥BC⇔ΔABC jest Δprostokątnym 2) Srodek AC jest środkiem okręgu opisanego na ΔABC S=(2,2) R=√5