trzy kolejne boki czworokąta opisanego na okręgu tworzą ciąg nataszka: Trzy kolejne boki czworokąta opisanego na okręgu tworzą ciąg geometryczny o pierwszym wyrazie 10 i sumie 70. Wyznacz długości boków tego czworokąta. Napiszę tu moje obliczenia do momentu, w którym pojawia się problem: s₄= 70 a₁=10 kolejne boki to a₁q a₁q² i a₁q³

	1−q4
40=10*
	1−q

	10−10q4
70=
	1−q

10−10q4		70−70q
	−		= 0
1−q		1−q

10−10q⁴−70+70q=o −10q⁴+70q−60=0 |: (−10) q⁴−7q+6=0 to podzieliłam przez q−1 hornerem i wyszło (q³+q²+q−6)(q−1)=o i dalej już nic nie wymyślę, nie umiem znaleźć już żadnych dzielników tego wielomianu, więc chyba robię gdzieś błąd, z góry dziękuję za pomoc

nataszka: już wszystko jasne, oczywiście tylko 3 boki tworzą ciag a ja liczyłam 4.

ejendi: jest ok, błędu nie ma, tylko trzeba wpaść na sposób to równanie ma cztery pierwiastki: dwa rzeczywiste i dawa urojone widać, że q1=1 drugi znalazłem na piechotę, najbliższa wartość q2=1,3891 też mam zaćmę, bo chodzi o wyliczenie jakby oprocentowania i pamiętam, że to się robiło przez logarytmowanie

ejendi: no własnie, a ja zajałem sie równaniem a nie treścią!

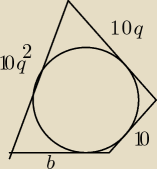
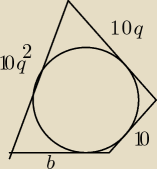Aga1: q>0 i b>0 10+10q+10q²+b=70 −−−3 boki tworzą ciąg geometryczny, a nie 4. 10+10q²=10q+b −−−własność czworokąta opisanego na okręgu