zad
MAcias: | | 1 | |
Wyznacz w zależności od parametru m liczbę rozwiązań równania | |
| − 3|+ m = 0 |
| | 3x | |
4 mar 17:16
rumpek:
Maturka z zadania.info

wczoraj robiłem
| | ⎧ | 0 dla m > 0 | |
| k(m) = | ⎨ | 1 dla m∊{0}U(−∞,−3> |
|
| | ⎩ | 2 dla m∊(−3,0) | |
Wskazówka:
|3
−x − 3| = −m / * (−1)
−|3
−x − 3| = m
Narysuj wykres 3
−x przesunięty o 3 jednostki w dół, potem odbij względem osi O
x, i jeszcze
potem odbij pod O
x i odczytać

4 mar 17:20
tp: Zgadza się

oto moje rozwiązania:
0 rozw dla m∊(0,
∞)
2 rozw dla m∊(−3,0)
1 rozw dla m∊{0}u(−
∞,3>
w porządku? mozesz jakos wysłać mi wszystkie rozwiązania?

4 mar 17:23
MAcias: I jaka dla Cb była ta maturka?
4 mar 17:26
rumpek: nie mam skanera

4 mar 17:26
MAcias: dobre te wyniki tu wyżej?
4 mar 17:30
rumpek:
Ale moje odp, to:
Zad 1. − tak jak wyzej
Zad. 2 dowód
Zad. 3 12
Zad. 4 −2
Zad. 5 2152064
| | π | | 2π | | 4π | | 5π | |
Zad. 6 { |
| , |
| , |
| , |
| } |
| | 3 | | 3 | | 3 | | 3 | |
Zad. 7 dowód
| | 9 | | 9√2π | |
Zad. 8 Boki: 2x |
| i 3 V = |
| |
| | 2 | | 4 | |
Zad. 9 |CD| = 2
√10 i C = (−5,7) D = (−7,1)
Zad. 11 6
√13 + 20
√6
4 mar 17:30
4 mar 17:32
Eta:
@rumpek
zad2/ 444....4 888.....9 = 444....48888...8 +1
Ja rozwiązałabym tak:
kwadrat każdej liczby naturalnej jest postaci 3k lub 3k+1
zatem suma cyfr tej liczby jest: 4n+8n+1= 12n+1 = 3*k+1
c.n.u
4 mar 17:34
Eta:
zad 11/ z ze wzoru Herona
i mamy "migiem"

..
odp: P
b= 6
√13+20
√6
4 mar 17:37
rumpek:
MAcias pamiętaj o dziedzinie dla tg

4 mar 17:37
rumpek: nom

ale ja wolałem obliczyć wysokości

4 mar 17:37
rumpek: odnośnie zadanie 2
Eto chcesz zobaczyć jak autorzy to zrobili?

4 mar 17:38
rumpek: zadania* 2
4 mar 17:38
TOmek : Ja jakoś przekonałem sie do Aksjomatu

4 mar 17:38
Eta:
Czyli zaliczyłeś
"wycieczkę z Sopotu do Gdyni przez
LONDYN" 
4 mar 17:39
rumpek: 
4 mar 17:39
Eta:
Widziałam

4 mar 17:40
rumpek: przekombinowali

4 mar 17:40
Eta:
Dokładnie

4 mar 17:41
MAcias: Aa no tak.. a zad 11 za 6pkt było tak proste że myslałem że zle zrobiłem a tu ok

4 mar 17:41
MAcias: Macie abonamenty tam wykupine? ;>
4 mar 17:42
rumpek: A co
Eto sądzisz o zadania z geometrii analitycznej? Osobiście jakbym nie pomyślał nad
punktem b), że można zrobić wektorowo., to nie wpadłbym na to podobieństwo trójkątów

4 mar 17:42
Eta:
Sms−− ik

4 mar 17:42
rumpek: abonamenty − tak, wykupione − nie, gratiski za aktywność

4 mar 17:43
Eta:
Ejjj tam,, banalne

( zawsze w trapezie rozpatrujemy podobieństwo tych trójkątów
4 mar 17:44
MAcias: Jak podpunkt a w tym trapezie z przekątnymi? xD
4 mar 17:48
rumpek: Osobiście liczyłem na wyższy poziom, ta maturka strasznie podobna do tej z maja, tylko trzeba
było bardziej pomyśleć.
4 mar 17:48
Eta:
zad 9)
→ →
| | 1 | |
PΔABS = |
| | d(AS, BS)|=..... = 4 |
| | 2 | |
| | h1*√10 | | 8 | |
|AB|= √10 to h1 (ΔABS) : |
| =4 ⇒ h1= |
| |
| | 2 | | √10 | |
| | k*8 | |
htr= h1+h2 ⇒ h2= k*h1= |
| |
| | √10 | |
|AB|=
√10 to |CD|= k*
√10 i P
tr= 36
dokończ wyznacz k >0
4 mar 18:02
rumpek: Eto a masz jakiś inny sposób na 10? Bo też zrobiłem kombinacją, ale wpierw próbowałem
"ręcznie"

czyli sprawdzać warunki.
4 mar 18:05
TOmek : mam pytanko jak "3" ugryźć?
4 mar 18:22
rumpek: Tw. sinusów

4 mar 18:25
TOmek : aha

danke
4 mar 18:28
MAcias: Ponawiam o zadanie 3.
4 mar 19:13
rumpek: za 15−20 minut zrobię, jak skoncze uczyc się z polskiego

4 mar 19:14
4 mar 19:50
rumpek:
Okrąg opisany na trójkącie ABC ma promień 12. Oznaczmy sobie |BC| = a.
Rozpatrzmy teraz kąt |∡ADC| = 180
o − α − β ⇔ |∡ADC| = 180
o − (α + β).
Pozostało teraz skorzystać z wzoru redukcyjnego:
sin(180
o − (α + β)) = sin(α + β)
| | a | |
2 * 12 = |
| / * sin(α + β) |
| | sin(α + β) | |
a = 24sin(α + β).
Musimy otrzymać promień okręgu opisanego na trójkącie BHC (u mnie na rysunku − z treści
zadania to AHB, po prostu inne oznaczenia

)
Szukany promień również obliczymy z twierdzenia sinusów, jednakże wpierw zauważmy, że:
1
o |∡CBE| = 90
o − α [ponieważ w trójkącie BEC, który jest prostokątny (jedno z ramion jest
wysokością całego trójkąta BCD, które pada pod kątem prostym) i otrzymamy warunek:
|∡CBE| = 180
o − 90
o − α]
2
o Podobnie z kątem |∡BCF| = 90
o − β [uzasadnienie jak wyżej].
Pozostało połączyć te wiadomości w trójkącie BHC: |∡CHB| = 180
o − |∡CBE| − |∡BCF| ⇔
|∡CHB| = 180
o − 90
o + α − 90
o + β ⇔ |∡CHB| = α + β.
To teraz tylko tw. sinusów:
| | 24sin(α + β) | |
2R2 = |
| |
| | sin(α + β) | |
2R
2 = 24 / : 2
R
2 = 12
4 mar 20:01
rumpek: Dobra spadam na "Ranczo"

4 mar 20:03
Eta:

4 mar 20:15
rumpek: Eto patrzyłaś może na mój post 18:05

?
4 mar 20:16
MAcias: Dzięki!

4 mar 20:38
MAcias: Teraz dopiero patrze, popierdzieliłeś z tymi oznaczeniami xD ale może obczaje.
4 mar 21:48
MAcias: Ale ok już

4 mar 21:51
rumpek: ale napisałem, że inne oznaczenia. ktoś nie czyta ze zrozumieniem

4 mar 21:55
Święty: rumpek w wolnej chwili skrobnąłbyś jak to tam trzeba rozwiązać to zadanie z analitycznej z
arkusza zadan.info?

5 mar 22:54
rumpek: Eta dała dużą wskazówkę

ale mogę zaraz zrobić

5 mar 22:55
Święty: No tak, nie doczytałem. Możesz sobie darować

5 mar 23:00
rumpek: A już skończyłem prawie podpunkt a)

no trudno xD
5 mar 23:02
rumpek:
"W trapezie ABCD , w którym AB || CD , dane są wierzchołki A = (1,1),B = (2,4) oraz punkt
przecięcia przekątnych S = (− 1,3) . Pole trapezu jest równe 36.
a) Oblicz długość podstawy CD .
b) Wyznacz współrzędne wierzchołków C i D"
1
o |AB| =
√(2 − 1)2 + (4 − 1)2 =
√1 + 9 =
√10
Szukam równania prostej AB
y = 3x − 2 ⇒ −3x + y + 2 = 0
2
o Liczę odległość punkt S = (−1,3) od prostej AB
| | |−3 * −1 + 1 * 3 + 2| | | |3 + 3 + 2| | | 8 | | 8√10 | |
d = |
| = |
| = |
| = |
| |
| | √9 + 1 | | √10 | | √10 | | 10 | |
d = h
1
h = h
1 + h
2
h
2 = k*h
1
h = h
1 + k*h
1
h = h1(1 + k)
a =
√10
b = ka
b = k
√10
| | 8√10 | |
72 = (√10 + k√10) * |
| (1 + k) |
| | 10 | |
| | 8√10 | |
72 = √10(1 + k) * |
| (1 + k) |
| | 10 | |
| | (1 + k) * 8√100 (1 + k) | |
72 = |
| |
| | 10 | |
720 = (1 + k) * 80 * (1 + k)
9 = (1 + k)
2
3
2 = (1 + k)
2
1 + k = 3
k = 2
|CD| = 2
√10.
b) wystarczy tylko wektorowo pociągnąć:
2|AS| = |SC| (oczywiście nad tym strzałki, lecz nie wiem jak się tutaj je "tworzy"

)
2|BS| = |SD|
5 mar 23:14
rumpek: będzie dla potomnych

5 mar 23:14
Eta:
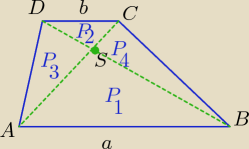
Można tak:
Z mojego (ulubionego) wzoru:
Ptr = (√P1+√P2)2 , gdzie
P3=P4= √P1*P2
→ →
| | 1 | |
|AB|= √10 P1= P(ΔABS)= |
| |d(AS, AB)|= ......... = 4 |
| | 2 | |
| P</td> | | √10 | | 4b2 | |
| = k2 = ( |
| )2 ⇒ P2= |
| |
| P2 | | b | | 10 | |
| | 4b2 | | 4b | |
to: P3=P4= √4* |
| = |
| |
| | 10 | | √10 | |
| | 4b | |
Ptr= 36 to: (√P1+√P2)2= 36 ⇒ 2+ |
| = 6 |
| | √10 | |
to: b= |CD|= 2
√10
| | b | |
zatem skala podobieństwa k >0 jest: k= |
| = 2 |
| | a | |
b) już prosto z wektorów :
→ → → →
SC= k*SA i SD= k*SB
5 mar 23:51
Eta:
Poprawiam zapis

5 mar 23:56
rumpek: Ta zależność z tymi polami jest bardzo ciekawa

nie uczą bowiem tego w szkole
5 mar 23:59
Eta:
A szkoda

6 mar 00:12
Eta:
Zależność prosta do wyjaśnienia:
P3=P4
Ptr= P1+P3+P4+P2 = P1+2P3+P2 = (√P1+√P2)2, P3=P4=√P1+P2
6 mar 00:17
 wczoraj robiłem
wczoraj robiłem

 oto moje rozwiązania:
0 rozw dla m∊(0, ∞)
2 rozw dla m∊(−3,0)
1 rozw dla m∊{0}u(−∞,3>
w porządku? mozesz jakos wysłać mi wszystkie rozwiązania?
oto moje rozwiązania:
0 rozw dla m∊(0, ∞)
2 rozw dla m∊(−3,0)
1 rozw dla m∊{0}u(−∞,3>
w porządku? mozesz jakos wysłać mi wszystkie rozwiązania? 

 ..
odp: Pb= 6√13+20√6
..
odp: Pb= 6√13+20√6

 ale ja wolałem obliczyć wysokości
ale ja wolałem obliczyć wysokości 











 ( zawsze w trapezie rozpatrujemy podobieństwo tych trójkątów
( zawsze w trapezie rozpatrujemy podobieństwo tych trójkątów
 czyli sprawdzać warunki.
czyli sprawdzać warunki.

 danke
danke

 )
Szukany promień również obliczymy z twierdzenia sinusów, jednakże wpierw zauważmy, że:
1o |∡CBE| = 90o − α [ponieważ w trójkącie BEC, który jest prostokątny (jedno z ramion jest
wysokością całego trójkąta BCD, które pada pod kątem prostym) i otrzymamy warunek:
|∡CBE| = 180o − 90o − α]
2o Podobnie z kątem |∡BCF| = 90o − β [uzasadnienie jak wyżej].
Pozostało połączyć te wiadomości w trójkącie BHC: |∡CHB| = 180o − |∡CBE| − |∡BCF| ⇔
|∡CHB| = 180o − 90o + α − 90o + β ⇔ |∡CHB| = α + β.
To teraz tylko tw. sinusów:
)
Szukany promień również obliczymy z twierdzenia sinusów, jednakże wpierw zauważmy, że:
1o |∡CBE| = 90o − α [ponieważ w trójkącie BEC, który jest prostokątny (jedno z ramion jest
wysokością całego trójkąta BCD, które pada pod kątem prostym) i otrzymamy warunek:
|∡CBE| = 180o − 90o − α]
2o Podobnie z kątem |∡BCF| = 90o − β [uzasadnienie jak wyżej].
Pozostało połączyć te wiadomości w trójkącie BHC: |∡CHB| = 180o − |∡CBE| − |∡BCF| ⇔
|∡CHB| = 180o − 90o + α − 90o + β ⇔ |∡CHB| = α + β.
To teraz tylko tw. sinusów:


 ?
?




 ale mogę zaraz zrobić
ale mogę zaraz zrobić 

 no trudno xD
no trudno xD
 )
2|BS| = |SD|
)
2|BS| = |SD|

 Można tak:
Z mojego (ulubionego) wzoru:
Ptr = (√P1+√P2)2 , gdzie P3=P4= √P1*P2
→ →
Można tak:
Z mojego (ulubionego) wzoru:
Ptr = (√P1+√P2)2 , gdzie P3=P4= √P1*P2
→ →

 nie uczą bowiem tego w szkole
nie uczą bowiem tego w szkole
