pomocyy Olka: jakie współrzędne ma obraz punktu P=(a,b) w symetri względem prostej y=2x ?

ejendi: wektor prostej y=2x −2x+y=0 w(A,B)=(−2,1) to jest wektor ⊥ do y=2x cosinusy kierunkowe wektora w

	A
cosα=
	|w|

|w|=√(−2)²+1²=√5

	−2
cosα=
	√5

	1
cosβ=
	√5

odległość P(a,b) od Y=2x

	−2a+b
d=
	√5

wektor wp zaczepiony w punkcie P

	−2(−2a+b)		4a−2b
Px=d*cosα=		=
	5		5

	−2a+b
Py=
	5

P'=P+2wp

	4a−2b
P'x=a+2Px=a+2*
	5

	−2a+b
P'y=b+2Py=b+2*
	5

ejendi: d=|wp|

Aga1:

	1−22		4
x'=		a+		b
	1+22		1+22

	4		1−22
y'=		a−		b
	1+22		1+22

ejendi: P'=P+2wp tu jest bład, powinno być P'=P−2wp, wektor przeciwny

	4a−2b		8a−4b
P'x=a−2Px=a−2*		=a−
	5		5

	−2a+b		4a−2b
P'y=b−2Py=b−2*		=b+
	5		5

po uproszczeniu:

	4b−3a
P'x=
	5

	4a−3b
P'y=
	5

ejendi: czyli to samo co podała Aga1, po uproszczeniu czy to jest wzór dla dowolnej prostej? 1 i 2 kojarzy się z wektorem (−2,1) a 4?

ejendi: kolejna poprawka, pisanie w tym edytorze jest męczliwe! P'y=(4a−3b)/5 powinien być + P'y=(4a+3b)/5 P'((4b−3a)/5,(4a+3b)/5)

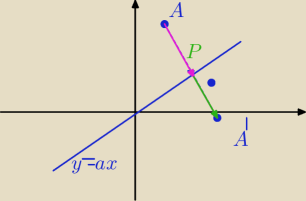
Aga1: Podałam Ci odp do Twojego zadania, A wzór . Obrazem punktu A(x,y) w symetrii względem prostej kk:y=ax jest punkt A^'(x^',y^') S_k(x,y)=(x^',y^') gdzie

	1−a2		2a
x'=		x+		y
	1+a2		1+a2

	2a		1−a2
y'=		x−		y
	1+a2		1+a2

AP^→=PA^'→ Nie znam wzorów na symetrię względem prostej y=ax+b.