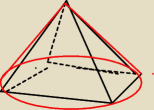
POMOCY OlAA: Na ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 6 i krawędzi bocznej 9 opisano stożek w sposób przedstawiony na rys. Oblicz objętość tego stożka

ANIA: proszę o pomoc

OLAA: potrafi ktoś rozwiązać to zadanie ? bo widzę że nie tylko ja go nie umiem rozwiązać

Krl: w ostsosłupie prawidłowym czworokątnym wysokość pada na przecięcie się przekątnych kwadratu. Promień stożka połowa przekątnej kwadratu. Mając przekątną i krawędź boczną liczysz wysokość z Pitagorasa

OLAA: hmm... ciemna magia

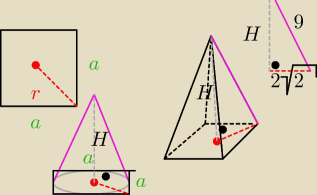
asdfdsasdf: a = 4 przekątna kwadratu = a √2 ⇒4√2 jeżeli 4√2 = średnica okręgu średnica okręgu = 2 promienie

	1
promień =		średnicy
	2

	1
promień =		* 4√2
	2

promień = 2√2 9 = krawędź boczna (oraz l − tworząca stożek) wszystko na rysunku

	1
V =		* πr2 * H
	3

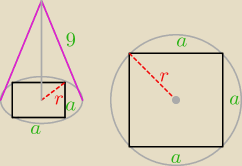
asdfdsasdf: poprawny rysunek stożka

OLAA: H = √73 ?

OLAA: CZY TYLE POWINNO WYJŚĆ ?

asdfdsasdf: tak

OLAA: to teraz jak to podstawie to wyjdzie jakiś okropny wynik

asdfdsasdf: w odpowiedzi jak jest?

OLAA: własnie o to chpdzi że nie mam odpowiedzi ale czy to możliwe żeby wysedł taki wynik

asdfdsasdf: ja tu nie widzę błędu, już po samym kwadracie wpisanym w koło (2 rysunek) widać wszystko

OLAA: czyli V= 3/8 * √73 pi

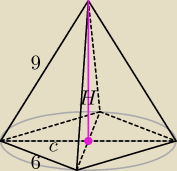
AAIO: c = 3√2, c² = 18 H = √81 − 18 = √63 = 3√7

	1		1
Objętość stożka V =		πc2*H =		π*18*3√7
	3		3

Mila: przekątna podstawy =6√2 r=3√2

asdfdsasdf: jaki głupi błąd nie wiem czemu, ale świtało mi w głowie 18.. (3√2)² = 18