ewelina: Dany jest okrąg o środku w początku układu współrzędnych i promieniu równym r oraz dwa przeciwległe wierzchołki kwadratu opisanego na tym okręgu. Uzasadnij, że suma kwadratów AM i BM nie zależy od punktu M należącego do okręgu.

b.: Trzeba wiedzieć, że trójkąt ABM jest zawsze prostokątny i zastosować tw. Pitagorasa.

beta: gówno prawda

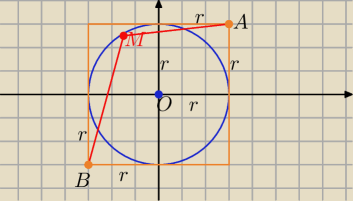
Eta: A(r,r) , B(−r,−r) M(x,y) i M∊o(O,r) ⇒ x²+y²=r² |AM|²+|BM|²= (x−r)²+(y−r)²+(x+r)²+(y+r)²=..... =2x²+2y²+4r²= =2(x²+y²)+4r²=2*r²+4r²= 6r² −−− zatem nie jest zależne od (x,y) punktu M c.n.u