podaj wzór funkcji ola: podaj wzór funkcji liniowej, której wykres przecina oś YO w punkcie (0,−3) i wraz z osiami układu współrzędnych ogranicza trójkąt o polu 18

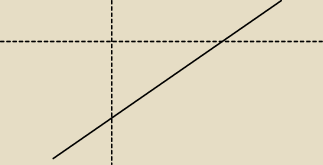
?: y=ax+b −3=a*0+b => b=−3 0=ax−3 => x=3/a 0,5*mod(−3)*(3/a) = 18 => 0,5*9/a=18 => 9/a=36 => a = 9/36 = 0,25 y=0,25*x−3

?:

ola: dziękuje bardzo już to trochę bardziej zrozumiałam

?: ogólny wzór na prostą to y=a*x+b prosta przecina os Y w punkcie minus 3, czyli do powyższego wzoru wstawiasz x=0 i y=−3 −3=a*0+b => b=−3 ( to jest współczynnik b równania prostej) teraz wyznaczamy punkt przecięcia z osią X: za y wstawiamy zero, a za b wstawiamy minus 3 który już znamy: 0=a*x−3 , stąd wyliczamy współrzędną x : x= 3/a teraz wzór na pole trójkąta P=0,5 * a*h . W naszym przypadku trójkąta prostokątnego P=0,5*długośćodcinka(0,a)*długośćodcinka(0,b) mod(−3) = moduł.liczby(−3) = −(−3)=3 czyli P=0,5*(3)*(3/a) => 18=3*3/(2*a) => 36=9/a => a= 9/36 => a=0,25 współczynnik b=−3 już mamy, i wstawiamy współczynniki a i b do równania prostej: y=0,25*x−3

ola: ok już rozumiem dziękuje bardzo