geometria analityczna ewelina11: 1. Napisz równanie okręgu o promieniu √5 stycznego do prostej o równaniu x−2y−1=0 w punkcie A=(3,1)

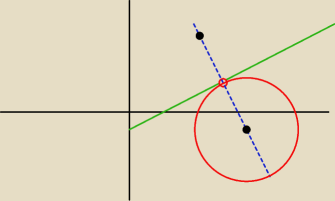
Tad: Niezdarny ten rysunek ... ale obrazować ma tylko, że są dwa takie okręgi ... −

Tad: dana prosta to y=x/2−1/2 prostopadła do niej ma współczynnik a=−2 ... a skoro przechodzi przez punkt A to .... y−1=−2(x−3) ... ⇒ ... y=−2x+7 Środek okręgu leży na tej prostej ... spełnia więc jej równanie ... ale jednocześnie √5=√(x_s−3)²+(y_s−1)² po rozwiązaniu x_s1=2 ... y_s1=3 x_s2=4 ... y_s2=−1 ... no i równania okręgów to już banał ...−