Geometria analityczna Ja:

	1
1. Na prostej o równaniu y=		x wyznacz punkty P i P' odległe o 4 od punktu R=(4,5).
	2

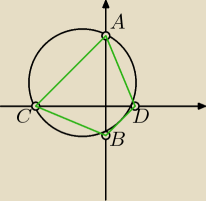
2. Dany jest okrąg o równaniu (x+7)²+(y−2)²=85. Punkty A i B są punktami przecięcia okręgu z osią OY, a punkty C i D − punktami przecięcia się z osią OX układu współrzędnych. Oblicz obwód i pole czworokąta ACBD.

Ja: Nie wiem jak się za to zabrać.

Aga1: 2.Trzeba wyliczyć współrzędne punktów A,B x=0, y=? C,D y=0, x=? Obwód to suma długości boków, które wyliczysz ze wzoru na odległość dwóch punktów (długość odcinka) P0le czworokąta to suma pól np trójkątów CDA i CDB

Aga1:

	1		1
1)Punkt leżący na prostej y=		x ma współrzędne P=(x,		x)
	2		2

IRPI=4

	1
√(x−4)2+(		x−5)2=4//2 (lewa strona jest cała pod pierwiastkiem)
	2

	1
(x−4)2+(		x−5)2=16
	2

dokończ.