....
ona^^: W urnie A jest 5 kul białych i 3 czarne ,w urnie B są 4 kule białe i 6 czarnych,Losujemy po
jednej kuli z każdej urny,Oblicz prawdopodobieństwo ,że wyjmiemy kule w jednym kolorze,Wynik
przestaw w postaci ułamku nieskracalnego .
i trzeba to zrobisz z sposobem jakiegoś drzewka

:(
2 mar 20:29
123:
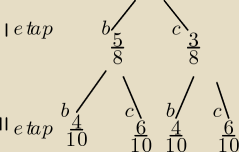
I. Sposób
|Ω| = C
18*C
110 = 8*10 = 80
|A| = C
15*C
16 + C
13*C
14 = 5*6 + 3*4 = 30 +12 = 42
| | 42 | | 21 | |
P(A) = |
| = |
| ≈ 0,53 |
| | 80 | | 40 | |
II. Sposób
Drzewko (mnożymy po gałęziach):
| | 5 | | 6 | | 3 | | 4 | | 30 | | 12 | |
P(A) = |
| * |
| + |
| * |
| = |
| + |
| = |
| | 8 | | 10 | | 8 | | 10 | | 80 | | 80 | |
2 mar 21:26
123: Oj... zrobiłem dla kul o różnym kolorze ale to nie szkodzi, bo prawdopodobieństwo o jednym
kolorze wynosi:
P(B) = 1 − P(A)
| | 21 | | 19 | |
P(B) = 1 − |
| = |
| ≈ 0,48 |
| | 40 | | 40 | |
2 mar 21:29
123: A co do drzewka to:
| | 5 | | 4 | | 3 | | 6 | | 20 | | 18 | | 38 | | 19 | |
P(B) = |
| * |
| + |
| * |
| = |
| + |
| = |
| = |
| ≈ |
| | 8 | | 10 | | 8 | | 10 | | 80 | | 80 | | 80 | | 40 | |
0,48
Jak widać to samo

2 mar 21:32
ona^^: a jak będzie w urnie jest 7 kul białych i 3 czarne,Losujemy z tej urny jedna kulę ,a następnie
z pozostałych kul znowu losujemy jedną .Oblicz prawdopodobieństwo .ze w ten sposób wyjmiemy
kule w różnych kolorach.Wynik przestaw w postaci ułamka nieskracalnego ...a to jak

?
2 mar 21:52
2 mar 21:56
ona^^: Dziękuje wam za drzewka . zd.3 .
Ze zbioru cyfr{0.1,2....,9}losujemy trzy razy po jednej cyfrze bez zwracania i układamy w
kolejności losowania w liczbę trzycyfrową.Oblicz prawdopodobieństwo ,że w ten sposób ułożymy
liczbę większą od 400.Wynik przestaw w postaci ułamku nieskracalnego ....A to niby jak ,
metoda jakiś kubków


2 mar 22:03
123: To liczymy tak:
|Ω| = 9*8*7 = 504
|A| = 1*1*8 + 1*8*9 + 4*9*9 = 8 + 72 + 324 = 404
Dlaczego?
1*1*8 − x y z, gdzie x (tylko 4), y (tylko 0), z (od 1 do 9 bez 0)
1*8*9 − x y z, gdzie x (tylko 4), y (od 1 do 9 bez 0), z (od 0 do 9)
4*9*9 − x y z, gdzie x (od 5 do 9), y (od 0 do 9), z (od 0 do 9)
2 mar 22:18
123: Boże co ja zrobiłem... Obliczyłem |A| ze zwracaniem...
2 mar 22:19
ona^^: i to jest dobrze

2 mar 22:19
123: Poczekaj chwilę to poprawię bo źle zrobiłem

2 mar 22:24
123: |Ω| = 9*8*7 = 504
|A| = 1*1*8 + 1*8*7 + 5*9*8 = 8 + 56 + 360 = 424
I. 1*1*8 − x*y*z, gdzie x (tylko 4), y (tylko 0), z ( liczba ze zbioru 0..9 BEZ 4 i 0)
II. 1*8*7 − x*y*z, gdzie x (tylko 4), y ( liczba ze zbioru 0..9 BEZ 0 i 4), z (liczba ze
zbioru 0..9 BEZ 4, 0 i wcześniej wybranej liczby "y")
III. 5*9*8 − x*y*z, gdzie x (liczba od 5..9), y (liczba ze zbioru 0..9 BEZ wcześniej wybranej
liczby "x"), z (liczba ze zbioru 0..9 BEZ wcześniej wybranych liczb: "x" i "y")
| | 424 | | 106 | | 53 | |
P(A) = |
| = |
| = |
| |
| | 504 | | 126 | | 63 | |
2 mar 22:35
123: OMG

! "|A|| dobrze wyliczone tylko |Ω| źle

!
Powinno być: |Ω| = 9*9*8 = 648
| | 424 | | 106 | | 53 | |
czyli P(A) = |
| = |
| = |
| |
| | 648 | | 162 | | 81 | |
teraz chyba dobrze... przepraszam ale już zmęczony jestem
2 mar 22:39
123: PODSUMOWUJĄC

|Ω| = 9*9*8 = 648
|A| = 1*1*8 + 1*8*7 + 5*9*8 = 8 + 56 + 360 = 424
I. 1*1*8 − x*y*z, gdzie x (tylko 4), y (tylko 0), z ( liczba ze zbioru 0..9 BEZ 4 i 0)
II. 1*8*7 − x*y*z, gdzie x (tylko 4), y ( liczba ze zbioru 0..9 BEZ 0 i 4), z (liczba ze zbioru
0..9 BEZ 4, 0 i wcześniej wybranej liczby "y")
III. 5*9*8 − x*y*z, gdzie x (liczba od 5..9), y (liczba ze zbioru 0..9 BEZ wcześniej wybranej
liczby "x"), z (liczba ze zbioru 0..9 BEZ wcześniej wybranych liczb: "x" i "y")
2 mar 22:42
ona^^: i tak dziękuje


idz spac bo sie nie wyśpisz

2 mar 22:42
123: jeszcze się trzymam

2 mar 22:44
 :(
:(
 I. Sposób
|Ω| = C18*C110 = 8*10 = 80
|A| = C15*C16 + C13*C14 = 5*6 + 3*4 = 30 +12 = 42
I. Sposób
|Ω| = C18*C110 = 8*10 = 80
|A| = C15*C16 + C13*C14 = 5*6 + 3*4 = 30 +12 = 42

 ?
?




 ! "|A|| dobrze wyliczone tylko |Ω| źle
! "|A|| dobrze wyliczone tylko |Ω| źle !
Powinno być: |Ω| = 9*9*8 = 648
!
Powinno być: |Ω| = 9*9*8 = 648
 |Ω| = 9*9*8 = 648
|A| = 1*1*8 + 1*8*7 + 5*9*8 = 8 + 56 + 360 = 424
I. 1*1*8 − x*y*z, gdzie x (tylko 4), y (tylko 0), z ( liczba ze zbioru 0..9 BEZ 4 i 0)
II. 1*8*7 − x*y*z, gdzie x (tylko 4), y ( liczba ze zbioru 0..9 BEZ 0 i 4), z (liczba ze zbioru
0..9 BEZ 4, 0 i wcześniej wybranej liczby "y")
III. 5*9*8 − x*y*z, gdzie x (liczba od 5..9), y (liczba ze zbioru 0..9 BEZ wcześniej wybranej
liczby "x"), z (liczba ze zbioru 0..9 BEZ wcześniej wybranych liczb: "x" i "y")
|Ω| = 9*9*8 = 648
|A| = 1*1*8 + 1*8*7 + 5*9*8 = 8 + 56 + 360 = 424
I. 1*1*8 − x*y*z, gdzie x (tylko 4), y (tylko 0), z ( liczba ze zbioru 0..9 BEZ 4 i 0)
II. 1*8*7 − x*y*z, gdzie x (tylko 4), y ( liczba ze zbioru 0..9 BEZ 0 i 4), z (liczba ze zbioru
0..9 BEZ 4, 0 i wcześniej wybranej liczby "y")
III. 5*9*8 − x*y*z, gdzie x (liczba od 5..9), y (liczba ze zbioru 0..9 BEZ wcześniej wybranej
liczby "x"), z (liczba ze zbioru 0..9 BEZ wcześniej wybranych liczb: "x" i "y")

 idz spac bo sie nie wyśpisz
idz spac bo sie nie wyśpisz 
