Kąty w czworokącie/trapezie - wyliczanie. Sasquie: zad.1 W czworokącie KLMN kąt LMN jest o 10 stopni większy od kąta KLM i o 20 stopni większy od kąta MNK, natomiast kąt NKL jest o 150% większy od kąta MNK. Oblicz miary kątów w tym czworokącie. zad. 2 W trapezie ABCD na jego dłuższej podstawie AB obrano punkt E taki, że DE||BC. Wiedząc, że kąt DEA=50 stopni oraz kąt ADE=60 stopni. Oblicz miary kątów wewnętrznych trapezu ABCD. Pozdrawiam

ejendi: 1) m=10+l m=20+n k=1,5n ⇔k=1,5(m−20) 360=k+l+m+n 360=1,5m−30+m−10+m+m−20 360=4,5m−60

	1
m=93
	3

	1
l=m−10=83
	3

	1
n=m−20=73
	3

k=1,5n 110,00 suma 360,00

ejendi: kątA=180−50−60=70 B=E=50 D=50+60=110 C=180−50=130 A+B+C+D=70+50+110+130=360

Aga1: 1) Czy kąt k jest większy o 150% od kąta n?

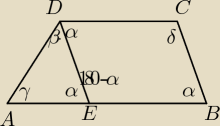
Aga1: α=50⁰, β=60⁰, γ=180−(α+β), bo suma kątów wewnętrznych w trójkącie wynosi 180⁰, a w czworokącie 360⁰. 2α+180−α+δ=360⁰