Tw. Sinusów i cosinusów Ola: Tw. Sinusów i cosinusów Ola: Przekrój poprzeczny tortu jest trójkątem równoramiennym. Uzasadnij, że jeśli pokroimy tort wzdłuż środkowych boków trójkąta to każdy otrzyma jedną z sześciu równych części.

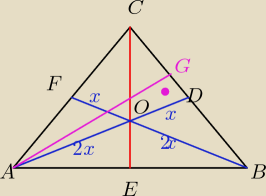
Aga1: Niech IABI=a i IACI=IBCI=b Środkowa ICEI=s=h . Środkowe w trójkącie dzielą się w stosunku 2:1 licząc od wierzchołka kąta, więc

	1
IOEI=		h
	3

i IADI=IBFI=s₁ Wśród tych trójkątów są trójkąty przystające ( wynika to z cechy b,b,b) o równych polach. wysokość IAGI=h₁

	1
h2=b2−(		a)2
	2

	√4b2−a2
h=
	2

α=kąt ACB Z twierdzenia cosinusów w trójkącie ABC a²=b²+b²−2b²cosα

	2b2−a2
cosα=
	2b2

W trójkącie ADC z twierdzenia cosinusów

	1		1		2b2−a2
s12=b2+(		b)2−2b*		b*
	2		2		2b2

	1		1
s12=b2+		b2−b2+		a2
	4		2

	√b2+2a2
s1=
	2

Pole EBO=P_AEO

	1		1		1	√4b2−a2		a
PAEO=		*		a*			=		√4b2−a2
	2		2		3	2		24

	1		a
PABC=		a*h=		√4b2−a2 oraz
	2		4

	1
PABC=		b*h1
	2

Stąd

1		a		1
	bh1=		√4b2−a2//:		b
2		4		2

	a
h1=		√4b2−a2
	2b

	1		1		1		a		a
PABD=		*		b*h1=		b*		√4b2−a2=		√4b2−a2
	2		2		4		2b		8

P_BDO=P_AFO P_BDO=P_ABD−2*P_BEO

	1		1		1
PBDO=		a√4b2−a2−2*		a√4b2−a2=		a√b2−a2
	8		24		24

P_ACD=P_ABC−P_ABD

	1		1		1
PACD=		√4b2−a2−		√4b2−a2=		a√4b2−a2
	4		8		8

P_CDO=P_CFO

	PACD−PAFO
PCDO=
	2

	1		1		1		1
PCDO=		(		a√4b2−a2−		a√4b2−a2)=		a√4b2−a2
	2		8		24		24